Язык Wolfram Language™

Неоднородный пуассоновский процесс

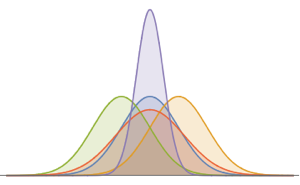
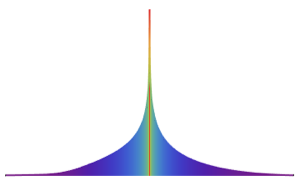
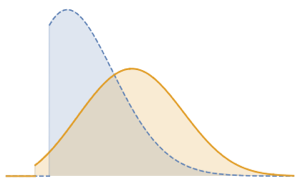
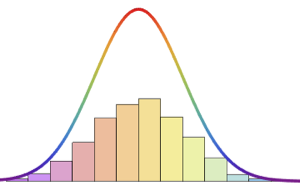
Неоднородный пуассоновский процесс является процессом Пуассона с изменяющейся во времени скоростью. Он может быть использован для моделирования времени посещения магазина покупателями, дорожно-транспортных процессов и проишествий. Функция плотности вероятности моделируемого процесса в любой момент времени t распределяется по принципу Пуассона.

In[1]:=

PDF[InhomogeneousPoissonProcess[f[\[Tau]], \[Tau]][t], x]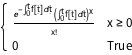

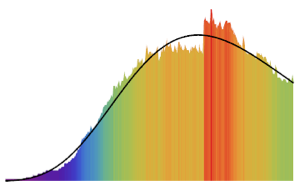
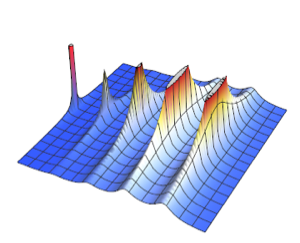
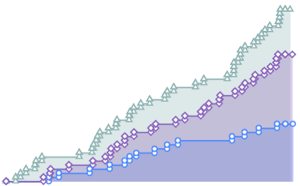
Out[1]=

Проведем симуляцию неоднородного пуассоновского процесса.

In[2]:=

td = RandomFunction[ InhomogeneousPoissonProcess[2 + 1/(1 + t^2), t], {0, 20}];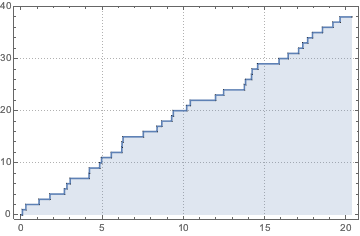

In[3]:=

ListStepPlot[td, Filling -> Axis, ImageSize -> Medium, PlotTheme -> "Detailed"]

Out[3]=

Hеоднородный пуассоновский процесс может быть использован для моделирования времени посещения магазина покупателями. В данном примере неоднородный пуассоновский процесс используется для моделирования количества клиентов в небольшом ресторане быстрого питания на основе почасовых данных о количестве клиентов в ресторане.

In[4]:=

arrivalrates = {{0, 8}, {1, 9}, {2, 7}, {4, 6}, {5, 12}, {6, 14}, {7, 11}, {8, 6}, {9, 4}, {10, 3}, {11, 8}, {12, 15}, {13, 12}, {14, 10}, {15, 8}, {16, 6}, {17, 12}, {18, 17}, {19, 15}, {20, 12}, {21, 6}, {22, 5}, {23, 7}}; \[Lambda][t_] = Interpolation[arrivalrates, InterpolationOrder -> 1][t];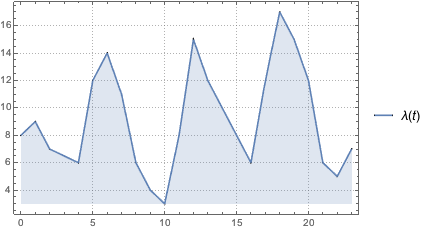

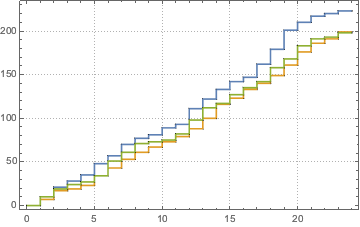
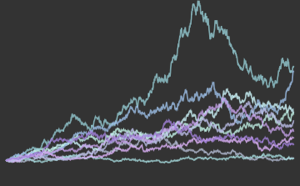
In[5]:=

Plot[\[Lambda][t], {t, 0, 23}, Exclusions -> None, Filling -> Axis, ImageSize -> Medium, PlotTheme -> "Detailed"]

Out[5]=

Воспользуемся неоднородным пуассоновским процессом на основе заданной функции скорости λ(t) и смоделируем количество клиентов в ресторане в течение дня.

In[6]:=

\[ScriptCapitalP] = InhomogeneousPoissonProcess[\[Lambda][t], t]; td = RandomFunction[\[ScriptCapitalP], {0, 23, 1}, 3];

In[7]:=

ListStepPlot[td, ImageSize -> Medium, PlotTheme -> "Detailed"]

Out[7]=