Точки разрыва в функции распределения вероятностей

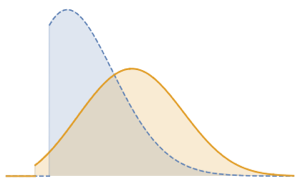
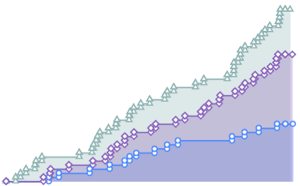
Зададим формулу распределения с помощью кумулятивной функции. Полученная функция содержит точки разрыва и представляет собой смесь непрерывных и дискретных компонентов.

In[1]:=

cdf = CDF[ MixtureDistribution[{1/3, 2/3}, {LaplaceDistribution[0, 1], TransformedDistribution[x - 2, x \[Distributed] BinomialDistribution[4, 1/3]]}], z];

In[2]:=

Plot[cdf, {z, -5, 5}, PlotTheme -> "Detailed", Filling -> Axis, ImageSize -> Medium, PlotLegends -> None]

Out[2]=

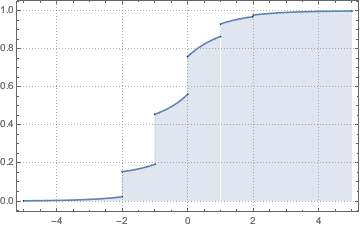
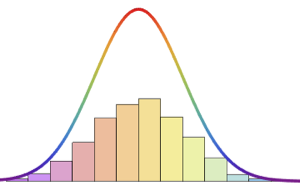
Функция ProbabilityDistribution разбивает распределение на непрерывные и дискретные сегменты.

In[3]:=

ProbabilityDistribution[{CDF, cdf}, {z, -Infinity, Infinity}]

Out[3]=

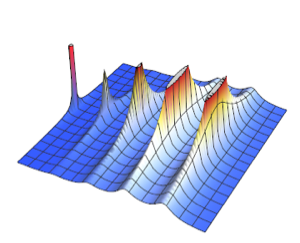
Продолжим работу с функцией распределения вероятностей с помощью функции DiracDelta.

In[4]:=

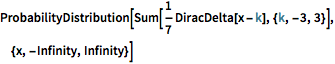
ProbabilityDistribution[ Sum[1/7 DiracDelta[x - k], {k, -3, 3}], {x, -Infinity, Infinity}]

Out[4]=