Wolfram Language™

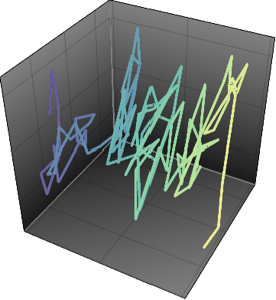
Brownsche Bewegung auf einem CUE

Eine Brownsche Bewegung auf dem Vielfachen der Einheitsmatritzen kann durch infinitesimale Generatoren aus Gaußschen unitären Ensembles erzeugt werden. Die stationäre Verteilung dieser Brownschen Bewegung ist dann identisch mit der Verteilung des CUE.

In[1]:=

mats = RandomVariate[GaussianUnitaryMatrixDistribution[0.1, 2], 100000]; mats = Table[MatrixExp[I mat], {mat, mats}];

Generieren Sie einen Brownschen Pfad mit Anfangpunkten eines CUE.

In[2]:=

initial = RandomVariate[CircularUnitaryMatrixDistribution[2]]; res = FoldList[#2.#1 &, initial, mats];

Berechnen Sie die Phasen der Eigenwerte und vergleichen Sie diese mit der WDF der Eigenwerte der Matritzen eines CUE.

In[3]:=

phases = RandomSample /@ Arg[Eigenvalues /@ res];

In[4]:=

Show[ ContourPlot[ 1/(8 Pi^2) Abs[Exp[I \[Phi]1] - Exp[I \[Phi]2]]^2, {\[Phi]1, -Pi, Pi}, {\[Phi]2, -Pi, Pi}], ListPlot[Take[phases, {1, -1, 10}], ImageSize -> Medium, PlotStyle -> Black, PlotTheme -> "Detailed"], ImageSize -> Medium]

Out[4]=