Wolfram Language™

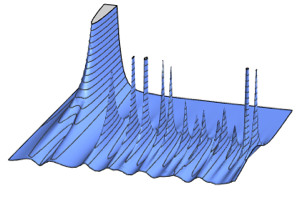
Séparations de valeurs propres de lois de Gauss

Les écarts entre les valeurs propres (différences entre les valeurs propres consécutives) des distributions matricielles ont une forme limite universelle qui est observée dans de nombreux systèmes naturels, tels que les écarts entre les niveaux d'énergie des atomes lourds.

Échantillonnez l'espacement des valeurs propres de matrices 2×2 provenant de différents ensembles gaussiens.

In[1]:=

gaussiandists = {GaussianOrthogonalMatrixDistribution[2], GaussianUnitaryMatrixDistribution[2], GaussianSymplecticMatrixDistribution[2]};

In[2]:=

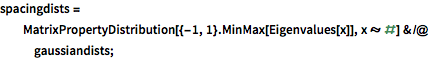
spacingdists = MatrixPropertyDistribution[{-1, 1}.MinMax[Eigenvalues[x]], x \[Distributed] #] & /@ gaussiandists;

In[3]:=

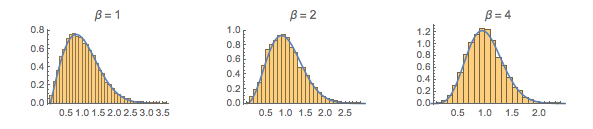
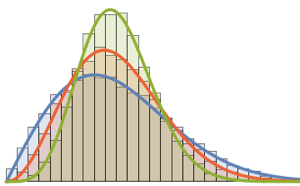
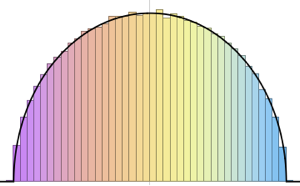
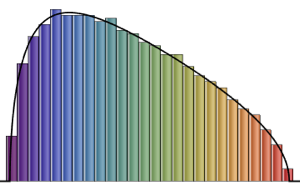
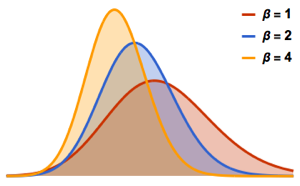
gaps = Normalize[RandomVariate[#, 10000], Mean] & /@ spacingdists;

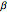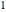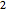Comparez les histogrammes de chaque distribution avec leur forme fermée, également connue sous le nom de supposition de Wigner pour les indices de Dyson de , et de .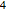

In[4]:=

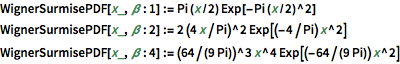
WignerSurmisePDF[x_, \[Beta] : 1] := Pi (x/2) Exp[-Pi (x/2)^2] WignerSurmisePDF[x_, \[Beta] : 2] := 2 (4 x/Pi)^2 Exp[(-4/Pi) x^2] WignerSurmisePDF[ x_, \[Beta] : 4] := (64/(9 Pi))^3 x^4 Exp[(-64/(9 Pi)) x^2]

In[5]:=

histogram = Histogram[#, {0.1}, PDF] & /@ gaps; plot = Plot[WignerSurmisePDF[x, #] , {x, 0, 3}] & /@ {1, 2, 4}; GraphicsRow@ MapThread[ Show[#1, #2, ImageSize -> 180, PlotLabel -> Row[{"\[Beta] = ", #3}]] &, {histogram, plot, {1, 2, 4}}]

Out[5]=