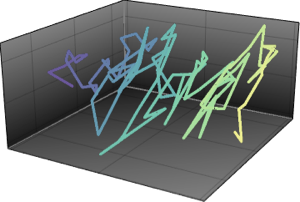
Gaz de Coulomb de Dyson

La loi commune des valeurs propres d'une matrice suivant CircularOrthogonalMatrixDistribution est équivalente à la loi de Boltzmann du gaz de Coulomb de Dyson sur un cercle avec la température inverse 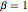. Définissez l'hamiltonien moyen (sans les termes cinétiques) par particule.

In[1]:=

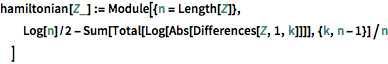
hamiltonian[Z_] := Module[{n = Length[Z]}, Log[n]/2 - Sum[Total[Log[Abs[Differences[Z, 1, k]]]], {k, n - 1}]/n ]

Définissez la distribution de l'hamiltonien.

In[2]:=

h\[ScriptCapitalD] = MatrixPropertyDistribution[hamiltonian[Eigenvalues[x]], x \[Distributed] CircularOrthogonalMatrixDistribution[n]];

Calculez la moyenne de l'échantillon de l'hamiltonien pour des systèmes de taille différente.

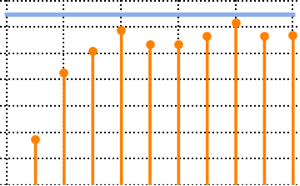
In[3]:=

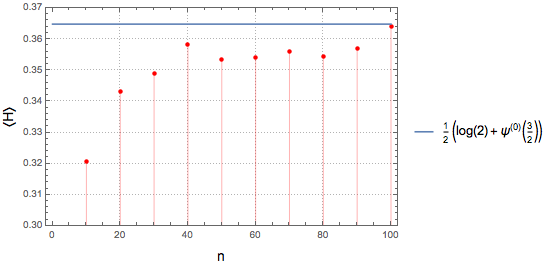
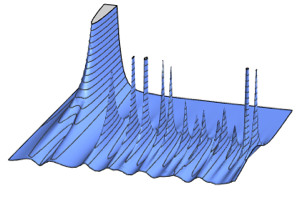
means = Table[{n, Mean[RandomVariate[h\[ScriptCapitalD], 1000]]}, {n, 10, 100, 10}];

Tracez les moyennes de l'échantillon et comparez-les à la limite thermodynamique.

In[4]:=

Show[ListPlot[means, PlotStyle -> {Red, PointSize[Medium]}, Filling -> Axis, PlotRange -> {0.3, 0.37}, FrameLabel -> {Style["n", Black, 14], Style["\[LeftAngleBracket]H\[RightAngleBracket]", Black, 14]}, PlotTheme -> "Detailed"], Plot[1/2 (Log[2] + PolyGamma[0, 3/2]), {x, 0, 100}, PlotTheme -> "Detailed"]]

Out[4]=