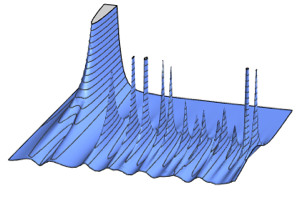
Propriétés de distributions matricielles

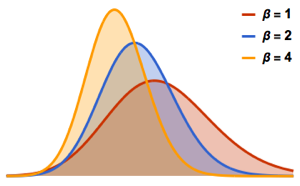
Les statistiques de plus faibles dimensions dérivées des matrices aléatoires jouent un rôle important dans la caractérisation des ensembles de matrice. Dans diverses situations de limites, les distributions de ces statistiques tombent dans différentes classes d'universalité. MatrixPropertyDistribution fournit un accès pratique à l'échantillon et le calcul de l'approximation numérique de ces propriétés dérivées.

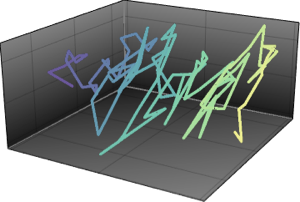
Prenez un échantillon des deux plus grandes valeurs propres à partir d'un ensemble unitaire gaussien.

In[1]:=

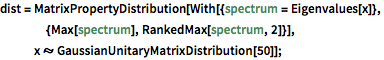
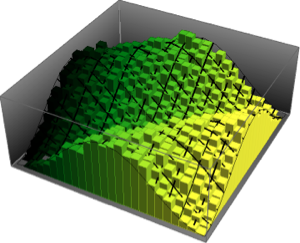
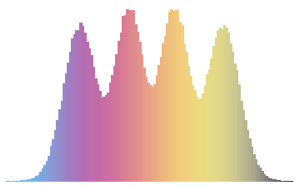
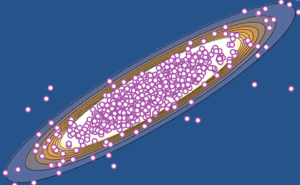
dist = MatrixPropertyDistribution[With[{spectrum = Eigenvalues[x]}, {Max[spectrum], RankedMax[spectrum, 2]}], x \[Distributed] GaussianUnitaryMatrixDistribution[50]];

In[2]:=

RandomVariate[dist]

Out[2]=

Visualisez la distribution conjointe des deux plus grandes valeurs propres sur la base du résultat échantillonné.

In[3]:=

sample = RandomVariate[dist, 10^4];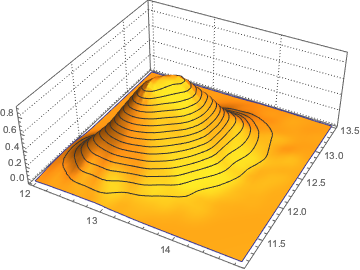

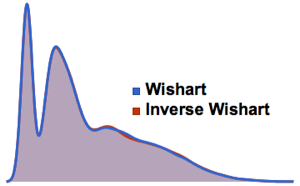
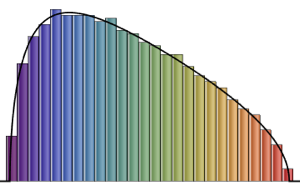
In[4]:=

SmoothHistogram3D[sample, "Scott", "PDF", PlotTheme -> "Detailed", ImageSize -> Medium]

Out[4]=

Prenez l'échantillonnage du déterminant de matrices à partir d'un ensemble orthogonal gaussien et comparez la loi empirique avec l'expression de forme fermée.

In[5]:=

dist = MatrixPropertyDistribution[Det[x], x \[Distributed] GaussianOrthogonalMatrixDistribution[2]]; dets = RandomVariate[dist, 10^6];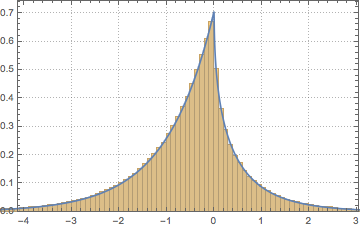

In[6]:=

empirical = Histogram[dets, {0.1}, PDF, PlotTheme -> "Detailed", ImageSize -> Medium]; detpdf[y_] := 1/Sqrt[2] Exp[ y] Piecewise[{{Erfc[Sqrt[2 y]], y >= 0}, {1, y < 0}}]; analytical = Plot[detpdf[y], {y, -5, 4}, Exclusions -> None, PlotLegends -> None, PlotTheme -> "Detailed", ImageSize -> Medium, Filling -> Axis]; Show[empirical, analytical]

Out[6]=

Approximez la moyenne du déterminant par un échantillonnage de Monte Carlo et comparez-la à la valeur réelle.

In[7]:=

{N@Mean[dist], Integrate[x detpdf[x], {x, -Infinity, Infinity}]}

Out[7]=