Wolfram Language™

Loi de Wishart et loi de Wishart inverse

La loi de Wishart est la loi de la matrice de covariance d'échantillons tirés de vecteurs aléatoires multinormaux indépendants. Il s'agit d'une généralisation de la distribution 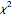à plusieurs dimensions. Cette loi apparaît naturellement dans les statistiques multivariées telles que la régression, la covariance, etc.

Générez une matrice positive aléatoire définie à utiliser comme paramètres pour la loi de Wishart.

In[1]:=

\[CapitalSigma] = DiagonalMatrix[RandomReal[10, 5]];

Les matrices de la loi de Wishart sont symétriques et définies positivement. »

In[2]:=

dist = WishartMatrixDistribution[30, \[CapitalSigma]]; mat = RandomVariate[dist];

In[3]:=

SymmetricMatrixQ[mat] && PositiveDefiniteMatrixQ[mat]

Out[3]=

La loi inverse de Wishart est la distribution matricielle inverse de la loi de Wishart. »

In[4]:=

invdist = InverseWishartMatrixDistribution[30, Inverse[\[CapitalSigma]]]; invmat = RandomVariate[invdist];

Les matrices de la loi inverse de Wishart sont symétriques et définies positivement.

In[5]:=

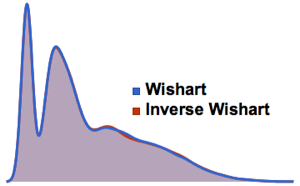
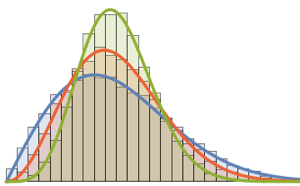
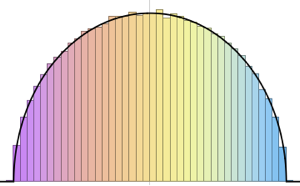
SymmetricMatrixQ[invmat] && PositiveDefiniteMatrixQ[invmat]

Out[5]=

Comparez la distribution des valeurs propres pour les matrices de la loi de Wishart et les lois de Wishart inverses.

In[6]:=

eigs = Flatten[ RandomVariate[ MatrixPropertyDistribution[Eigenvalues[x], x \[Distributed] dist], 10^4]]; inveigs = Flatten[RandomVariate[ MatrixPropertyDistribution[Eigenvalues[x]^-1, x \[Distributed] invdist], 10^4]];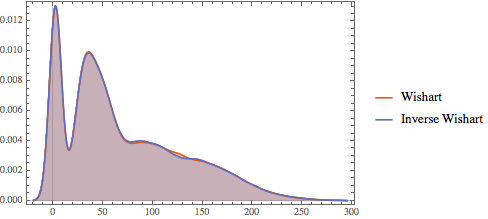

In[7]:=

SmoothHistogram[{eigs, inveigs}, PlotLegends -> {"Wishart", "Inverse Wishart"}, Filling -> Axis, ImageSize -> Medium, PlotTheme -> "Scientific"]

Out[7]=

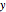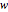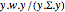Pour tout vecteur non nul et la matrice de Wishart avec la matrice d'échelle , la statistique est distribuée en .

In[8]:=

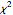y = #/Sqrt[#.\[CapitalSigma].#] &[RandomReal[1, 5]]; data = RandomVariate[ MatrixPropertyDistribution[y.w.y, w \[Distributed] WishartMatrixDistribution[30, \[CapitalSigma]]], 10^4];

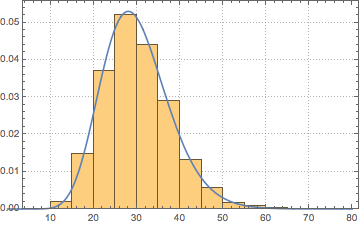
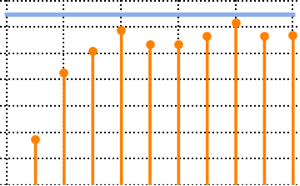
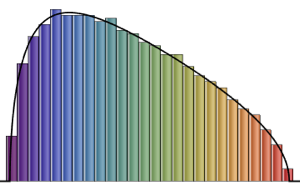
In[9]:=

Show[Histogram[data, Automatic, PDF, PlotTheme -> "Detailed"], Plot[PDF[ChiSquareDistribution[30], x], {x, 0, 80}], ImageSize -> Medium]

Out[9]=