Mouvement brownien sur CUE

Le mouvement brownien sur le collecteur des matrices unitaires peut être construit par des générateurs infinitésimaux à partir de l'ensemble unitaire gaussien. La loi stationnaire de ce mouvement brownien est alors identique à la loi du CUE.

In[1]:=

mats = RandomVariate[GaussianUnitaryMatrixDistribution[0.1, 2], 100000]; mats = Table[MatrixExp[I mat], {mat, mats}];

Générez un chemin brownien avec le point initial de l'échantillon de CUE.

In[2]:=

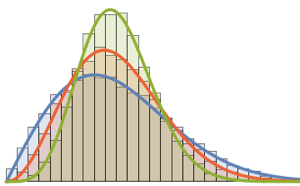
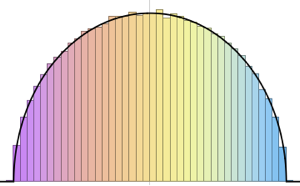
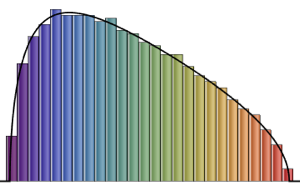
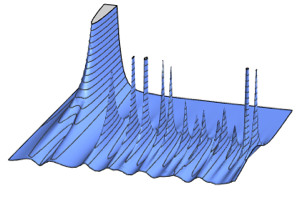
initial = RandomVariate[CircularUnitaryMatrixDistribution[2]]; res = FoldList[#2.#1 &, initial, mats];

Calculez les phases des valeurs propres et comparez-les à la fonction de probabilité des valeurs propres des matrices à partir de CUE.

In[3]:=

phases = RandomSample /@ Arg[Eigenvalues /@ res];

In[4]:=

Show[ ContourPlot[ 1/(8 Pi^2) Abs[Exp[I \[Phi]1] - Exp[I \[Phi]2]]^2, {\[Phi]1, -Pi, Pi}, {\[Phi]2, -Pi, Pi}], ListPlot[Take[phases, {1, -1, 10}], ImageSize -> Medium, PlotStyle -> Black, PlotTheme -> "Detailed"], ImageSize -> Medium]

Out[4]=