Wolfram Language™

Ensembles de Gauss (GOE, GUE...)

Les ensembles gaussiens sont des familles de matrices aléatoires normalement distribuées dont les distributions sont invariantes sous différentes transformations unitaires. Ils sont bien étudiés, en partie en raison de leur facilité d'analyse, mais aussi parce que les spectres associés se rapprochent étroitement de ceux de nombreux systèmes à grands degrés de liberté. Des exemples de ces systèmes apparaissent en physique, en finance et en biologie.

Les matrices de l'ensemble orthogonal gaussien (GOE) sont symétriques. »

In[1]:=

goe = RandomVariate[GaussianOrthogonalMatrixDistribution[5]];

In[2]:=

SymmetricMatrixQ[goe]

Out[2]=

Les matrices de l'ensemble unitaire gaussien (GUE) sont hermitiennes. »

In[3]:=

gue = RandomVariate[GaussianUnitaryMatrixDistribution[5]];

In[4]:=

HermitianMatrixQ[gue]

Out[4]=

Les matrices de l'ensemble symplectique gaussien (GSE) sont symplectiques hermitiennes. »

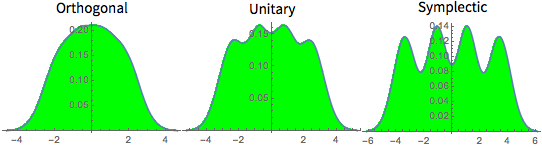
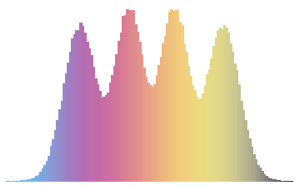
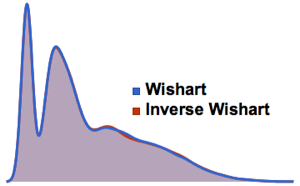
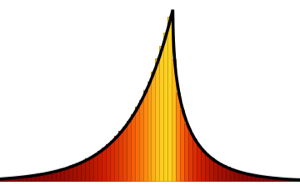
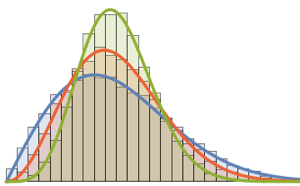
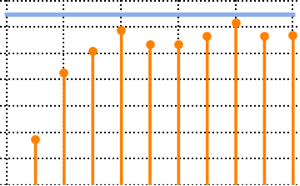
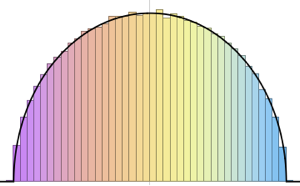
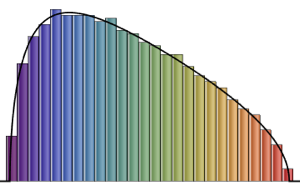
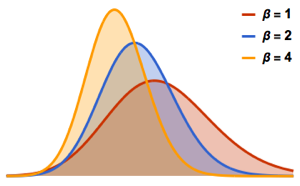
In[5]:=

symplecticMatrixQ[m_] := With[{\[ScriptCapitalJ] = KroneckerProduct[{{0, -1}, {1, 0}}, IdentityMatrix[Length[m]/2]]}, Conjugate[m].\[ScriptCapitalJ] == \[ScriptCapitalJ].m ];

In[6]:=

gse = RandomVariate[GaussianSymplecticMatrixDistribution[5]];

In[7]:=

symplecticMatrixQ[gse] && HermitianMatrixQ[gse]

Out[7]=

Distribution des valeurs propres pour les matrices des ensembles gaussiens à petites dimensions.

In[8]:=

eigs = Flatten[ RandomVariate[ MatrixPropertyDistribution[Eigenvalues[x], x \[Distributed] #], 10^5]] & /@ {GaussianOrthogonalMatrixDistribution[4], GaussianUnitaryMatrixDistribution[4], GaussianSymplecticMatrixDistribution[4]}; Row[MapThread[ SmoothHistogram[#1, "Scott", Frame -> None, PlotLegends -> Placed[#2, Above], Filling -> Axis, FillingStyle -> Green] &, {eigs, {Style["Orthogonal", 15], Style["Unitary", 15], Style["Symplectic", 15]}}]]

Out[8]=