Wolfram Language™

Loi de Marchenko–Pastur

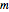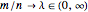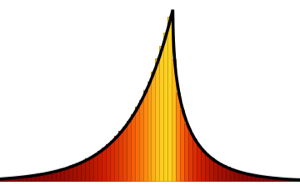
La loi de Marchenko-Pastur est la loi limite des valeurs propres des matrices de Wishart lorsque la dimension de la matrice et les degrés de liberté tendent tous deux vers l'infini avec le rapport . Pour 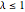, la distribution n'a pas de masse ponctuelle et la fonction de densité de probabilité est bien définie.

In[1]:=

PDF[MarchenkoPasturDistribution[1/2], x]

Out[1]=

In[2]:=

Plot[PDF[MarchenkoPasturDistribution[1/2], x], {x, 0, 3}, PlotRange -> All, Exclusions -> None, Filling -> Axis, PlotTheme -> "Detailed", ImageSize -> Medium, PlotLegends -> None]

Out[2]=

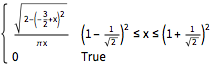
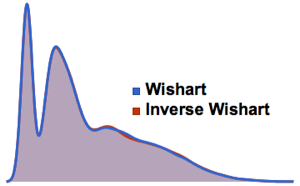
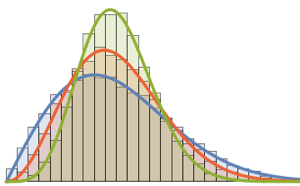
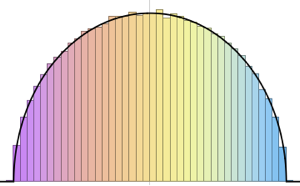
Échantillonnez à partir d'une loi de Wishart avec une matrice d'échelle identique et calculez les valeurs propres mises à l'échelle.

In[3]:=

n = 10^4; m = 10^3; eigs = RandomVariate[ MatrixPropertyDistribution[Eigenvalues[x]/n, x \[Distributed] WishartMatrixDistribution[n, IdentityMatrix[m]]]];

Comparez le résultat échantillonné avec la fonction de densité de Marchenko–Pastur.

In[4]:=

Show[Histogram[eigs, {0.05}, "PDF", ImageSize -> Medium, PlotTheme -> "Detailed"], Plot[PDF[MarchenkoPasturDistribution[m/n], x], {x, 0, 1.8}, PlotTheme -> "Detailed", PlotLegends -> None, Exclusions -> None]]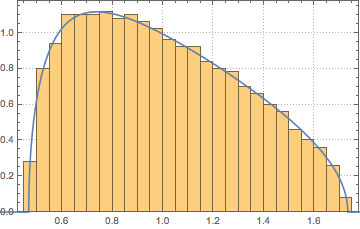

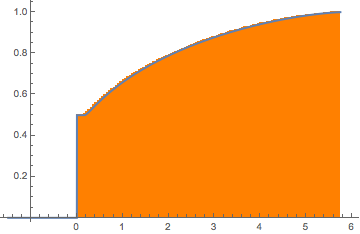
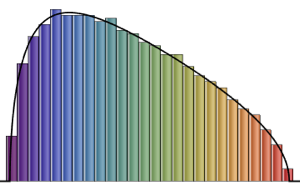
Out[4]=

Pour 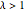, la matrice de Wishart est singulière. Avec la probabilité 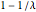, la distribution a une masse en .

In[5]:=

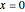m = 500; n = 2 m; CDF[MarchenkoPasturDistribution[n/m], 0]

Out[5]=

Générez une matrice de Wishart singulière avec une covariance identique et calculez les valeurs propres échelonnées.

In[6]:=

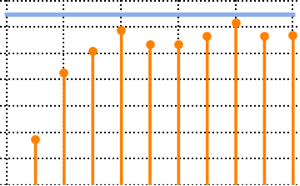
matrix = Transpose[#].# &[RandomVariate[NormalDistribution[], {m, n}]]; eigvs = Chop[Eigenvalues[matrix]/m];

Il y a un écart dans la densité des valeurs propres près de 0, et la case à 0 a une grande densité.

In[7]:=

Histogram[eigvs, {0.05}, PDF, PlotRange -> 1, ChartStyle -> Orange, ImageSize -> Medium]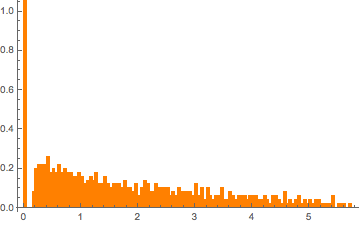

Out[7]=

Ajustez MarchenkoPasturDistribution aux valeurs propres.

In[8]:=

edist = EstimatedDistribution[eigvs, MarchenkoPasturDistribution[\[Lambda], 1]]

Out[8]=

La fonction de distribution cumulative de la loi ajustée montre une discontinuité de saut à l'origine.

In[9]:=

Show[Histogram[eigvs, {0.05}, CDF, ChartStyle -> Orange], Quiet@Plot[CDF[edist, x], {x, -1.5, 5.75}, Exclusions -> None, PlotStyle -> Thick], ImageSize -> Medium, AxesOrigin -> {-1, 0}, PlotRange -> {{-1.5, 6}, {0, 1}}]

Out[9]=