高斯系综（GOE、GUE、...）: Wolfram语言 11 的新功能

‹›

高斯系综（GOE、GUE、...）

高斯系综是在不同酉变换下分布不变的正态分布随机矩阵家族. 它们得以充分研究，部分原因是其解析求解能力，也因为相关谱与那些大自由度的许多系统非常接近. 这些系统的范例出现在物理、金融和生物学领域中.

由高斯正交系综（GOE）得到的矩阵是对称矩阵. »

In[1]:=

goe = RandomVariate[GaussianOrthogonalMatrixDistribution[5]];

In[2]:=

SymmetricMatrixQ[goe]

Out[2]=

由高斯酉系综（GUE）得到的矩阵是埃尔米特矩阵. »

In[3]:=

gue = RandomVariate[GaussianUnitaryMatrixDistribution[5]];

In[4]:=

HermitianMatrixQ[gue]

Out[4]=

由高斯辛系综（GSE）得到的矩阵是埃尔米特辛矩阵. »

显示完整的 Wolfram 语言输入

In[5]:=

symplecticMatrixQ[m_] := 
  With[{\[ScriptCapitalJ] = 
     KroneckerProduct[{{0, -1}, {1, 0}}, IdentityMatrix[Length[m]/2]]},
   Conjugate[m].\[ScriptCapitalJ] == \[ScriptCapitalJ].m
   ];

In[6]:=

gse = RandomVariate[GaussianSymplecticMatrixDistribution[5]];

In[7]:=

symplecticMatrixQ[gse] && HermitianMatrixQ[gse]

Out[7]=

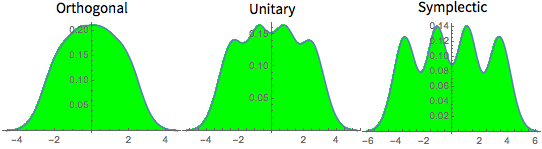
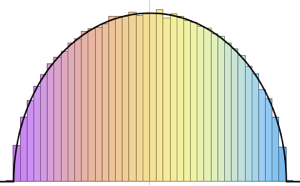
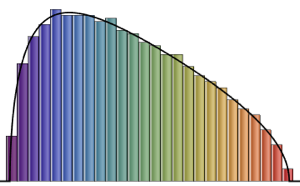
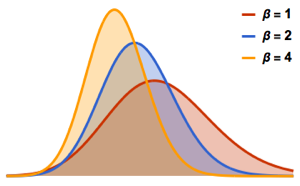
由小维度高斯系综得到的矩阵的特征值分布.

显示完整的 Wolfram 语言输入

In[8]:=

eigs = Flatten[
     RandomVariate[
      MatrixPropertyDistribution[Eigenvalues[x], x \[Distributed] #], 
      10^5]] & /@ {GaussianOrthogonalMatrixDistribution[4], 
    GaussianUnitaryMatrixDistribution[4], 
    GaussianSymplecticMatrixDistribution[4]};
Row[MapThread[
  SmoothHistogram[#1, "Scott", Frame -> None, 
    PlotLegends -> Placed[#2, Above], Filling -> Axis, 
    FillingStyle -> Green] &,
  {eigs, {Style["Orthogonal", 15], Style["Unitary", 15], 
    Style["Symplectic", 15]}}]]

Out[8]=

Wolfram 语言™

高斯系综（GOE、GUE、...）

相关范例