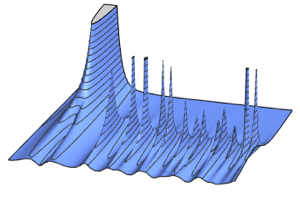
ガウス型アンサンブル(GOE，GUE，...)

ガウス型アンサンブルは正規分布するランダム行列族であり，分布はさまざまなユニタリ変換で不変である．これらは深く研究が行われているが，その理由のひとつは分析的に扱いやすいからである．それ以外にも，関連するスペクトルが，自由度の大きい数多くの系のスペクトルに非常に近いからという理由もある．このような系は物理学，金融学，生物学で使用される．

ガウス型直交アンサンブル(GOE)の行列は対称行列である． »

In[1]:=

goe = RandomVariate[GaussianOrthogonalMatrixDistribution[5]];

In[2]:=

SymmetricMatrixQ[goe]

Out[2]=

ガウス型ユニタリアンサンブル(GUE)はエルミート行列である． »

In[3]:=

gue = RandomVariate[GaussianUnitaryMatrixDistribution[5]];

In[4]:=

HermitianMatrixQ[gue]

Out[4]=

ガウス型シンプレクティックアンサンブル(GSE)はシンプレクティックエルミート行列である． »

In[5]:=

symplecticMatrixQ[m_] := With[{\[ScriptCapitalJ] = KroneckerProduct[{{0, -1}, {1, 0}}, IdentityMatrix[Length[m]/2]]}, Conjugate[m].\[ScriptCapitalJ] == \[ScriptCapitalJ].m ];

In[6]:=

gse = RandomVariate[GaussianSymplecticMatrixDistribution[5]];

In[7]:=

symplecticMatrixQ[gse] && HermitianMatrixQ[gse]

Out[7]=

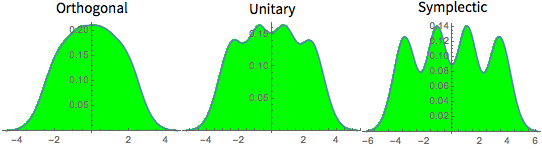
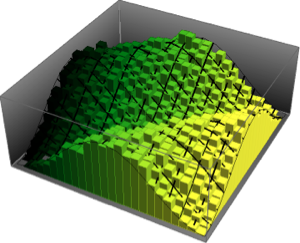
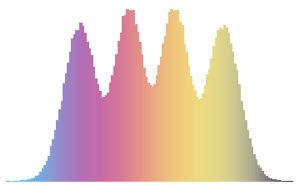
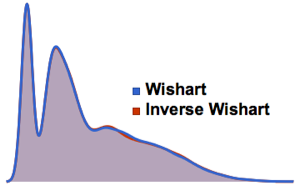
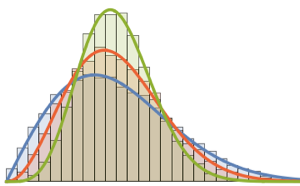
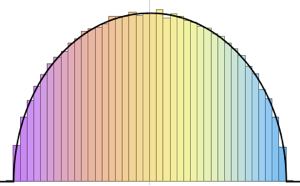
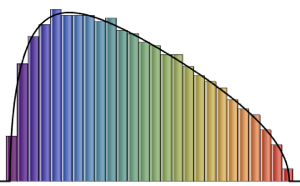
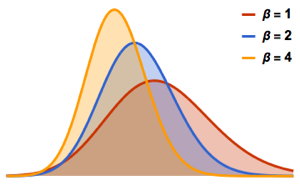
次元数の小さいガウス型アンサンブルの行列の固有値の分布．

In[8]:=

eigs = Flatten[ RandomVariate[ MatrixPropertyDistribution[Eigenvalues[x], x \[Distributed] #], 10^5]] & /@ {GaussianOrthogonalMatrixDistribution[4], GaussianUnitaryMatrixDistribution[4], GaussianSymplecticMatrixDistribution[4]}; Row[MapThread[ SmoothHistogram[#1, "Scott", Frame -> None, PlotLegends -> Placed[#2, Above], Filling -> Axis, FillingStyle -> Green] &, {eigs, {Style["Orthogonal", 15], Style["Unitary", 15], Style["Symplectic", 15]}}]]

Out[8]=