가우시안 앙상블 (GOE，GUE，...): Wolfram Language 11의 신기능

가우시안 앙상블 (GOE，GUE，...)

가우시안 앙상블은 정규 분포하는 랜덤 행렬이며 분포는 다양한 유니타리 변환에 불변합니다. 이에대한 깊은 연구가 이루어지고 있으며, 그 이유 중 하나로는 분석적으로 취급하기 용이하기 때문입니다. 이외에도 관련 스펙트럼이 자유도가 높은 복잡계에 매우 가깝기 때문이라는 이유도 있습니다. 이러한 시스템은 물리학, 금융, 생물학에서 주로 사용됩니다.

가우시안 직교 앙상블 (GOE)의 행렬은 대칭 행렬입니다. »

In[1]:=

goe = RandomVariate[GaussianOrthogonalMatrixDistribution[5]];

In[2]:=

SymmetricMatrixQ[goe]

Out[2]=

가우스시안 유니타리 앙상블 (GUE)은 에르미트 행렬입니다. »

In[3]:=

gue = RandomVariate[GaussianUnitaryMatrixDistribution[5]];

In[4]:=

HermitianMatrixQ[gue]

Out[4]=

가우시안 심플랙틱 앙상블 (GSE)은 심플랙틱 에르미트 행렬입니다. »

전체 Wolfram 언어 입력 표시하기

In[5]:=

symplecticMatrixQ[m_] := 
  With[{\[ScriptCapitalJ] = 
     KroneckerProduct[{{0, -1}, {1, 0}}, IdentityMatrix[Length[m]/2]]},
   Conjugate[m].\[ScriptCapitalJ] == \[ScriptCapitalJ].m
   ];

In[6]:=

gse = RandomVariate[GaussianSymplecticMatrixDistribution[5]];

In[7]:=

symplecticMatrixQ[gse] && HermitianMatrixQ[gse]

Out[7]=

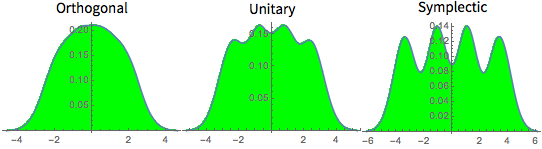
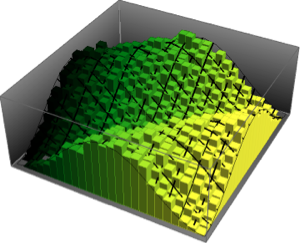
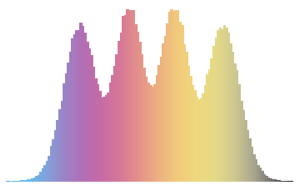
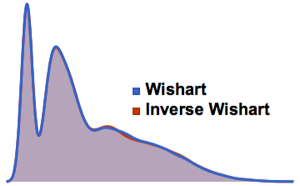
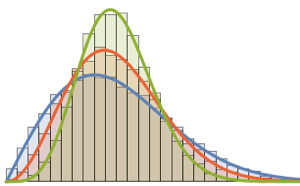
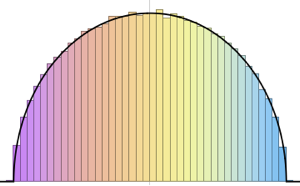
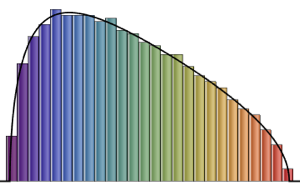
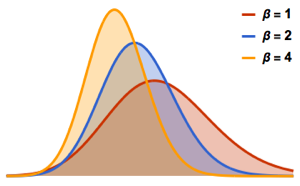
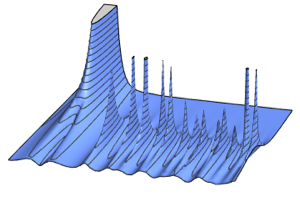
차원수가 작은 가우시안 앙상블의 행렬의 고유값의 분포입니다.

전체 Wolfram 언어 입력 표시하기

In[8]:=

eigs = Flatten[
     RandomVariate[
      MatrixPropertyDistribution[Eigenvalues[x], x \[Distributed] #], 
      10^5]] & /@ {GaussianOrthogonalMatrixDistribution[4], 
    GaussianUnitaryMatrixDistribution[4], 
    GaussianSymplecticMatrixDistribution[4]};
Row[MapThread[
  SmoothHistogram[#1, "Scott", Frame -> None, 
    PlotLegends -> Placed[#2, Above], Filling -> Axis, 
    FillingStyle -> Green] &,
  {eigs, {Style["Orthogonal", 15], Style["Unitary", 15], 
    Style["Symplectic", 15]}}]]

Out[8]=

Wolfram 언어™

가우시안 앙상블 (GOE，GUE，...)

관련 예제