Wolfram Language™

Gaußsche Ensembles (GOE, GUE, ...)

Ein Gaußsches Ensemble ist die Gesamtheit normalverteilter Zufallsmatritzen mit Verteilungen, die unter unterschiedlichen unitären Transformationen unveränderlich bleiben. Sie bilden wegen ihrer analytischen Lösbarkeit ein intensiv untersuchtes Gebiet, aber auch weil die mit ihnen verbundenen Spektren jene der Systeme mit vielen Freiheitsgraden stark approximieren. Diese Systeme treten beispielsweise in der Physik, Finanz und Biologie auf.

Matritzen des Gaußschen orthogonalen Ensembles (GOE) sind symmetrisch.»

In[1]:=

goe = RandomVariate[GaussianOrthogonalMatrixDistribution[5]];

In[2]:=

SymmetricMatrixQ[goe]

Out[2]=

Matritzen des Gaußschen unitären Ensembles (GUE) sind hermitesch.»

In[3]:=

gue = RandomVariate[GaussianUnitaryMatrixDistribution[5]];

In[4]:=

HermitianMatrixQ[gue]

Out[4]=

Matritzen des Gaußschen symplektischen Ensembles (GSE) sind symplektisch hermitesch.»

In[5]:=

symplecticMatrixQ[m_] := With[{\[ScriptCapitalJ] = KroneckerProduct[{{0, -1}, {1, 0}}, IdentityMatrix[Length[m]/2]]}, Conjugate[m].\[ScriptCapitalJ] == \[ScriptCapitalJ].m ];

In[6]:=

gse = RandomVariate[GaussianSymplecticMatrixDistribution[5]];

In[7]:=

symplecticMatrixQ[gse] && HermitianMatrixQ[gse]

Out[7]=

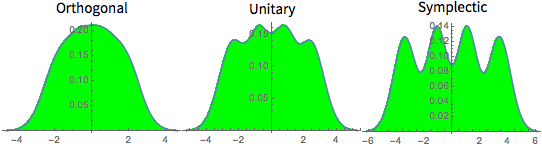
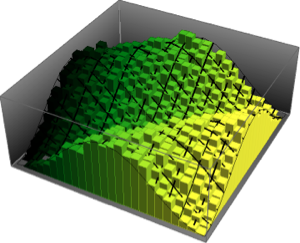
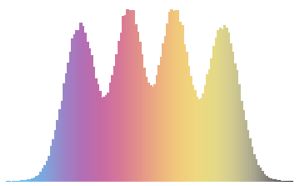
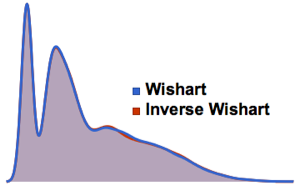
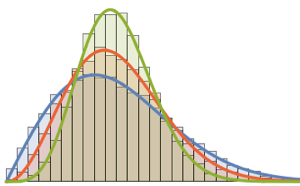
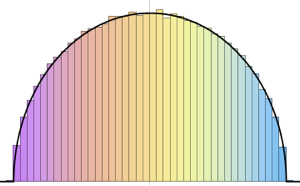
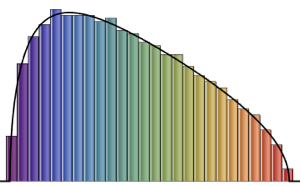
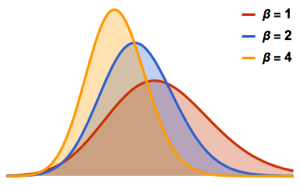
Eigenwertverteilung für Matritzen von Gaußschen Ensembles in kleinen Dimensionen.

In[8]:=

eigs = Flatten[ RandomVariate[ MatrixPropertyDistribution[Eigenvalues[x], x \[Distributed] #], 10^5]] & /@ {GaussianOrthogonalMatrixDistribution[4], GaussianUnitaryMatrixDistribution[4], GaussianSymplecticMatrixDistribution[4]}; Row[MapThread[ SmoothHistogram[#1, "Scott", Frame -> None, PlotLegends -> Placed[#2, Above], Filling -> Axis, FillingStyle -> Green] &, {eigs, {Style["Orthogonal", 15], Style["Unitary", 15], Style["Symplectic", 15]}}]]

Out[8]=