Wolfram Language™

Marchenko–Pastur Distribution

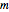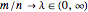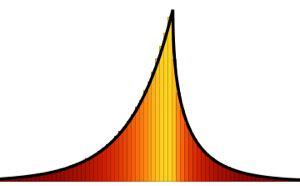
Marchenko–Pastur distribution is the limiting distribution of eigenvalues of Wishart matrices as the matrix dimension and degrees of freedom both tend to infinity with ratio . For , the distribution has no point mass and the probability density function is well-defined.

In[1]:=

PDF[MarchenkoPasturDistribution[1/2], x]

Out[1]=

In[2]:=

Plot[PDF[MarchenkoPasturDistribution[1/2], x], {x, 0, 3}, PlotRange -> All, Exclusions -> None, Filling -> Axis, PlotTheme -> "Detailed", ImageSize -> Medium, PlotLegends -> None]

Out[2]=

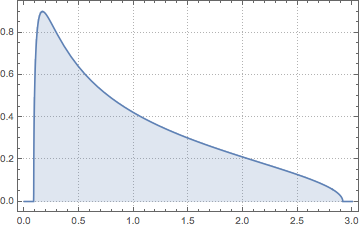
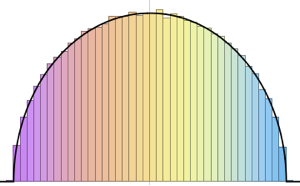
Sample from a Wishart distribution with identity scale matrix and compute the scaled eigenvalues.

In[3]:=

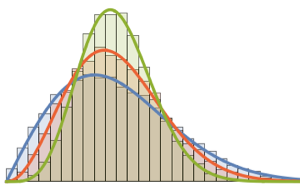
n = 10^4; m = 10^3; eigs = RandomVariate[ MatrixPropertyDistribution[Eigenvalues[x]/n, x \[Distributed] WishartMatrixDistribution[n, IdentityMatrix[m]]]];

Compare the sampled result with the Marchenko–Pastur density function.

In[4]:=

Show[Histogram[eigs, {0.05}, "PDF", ImageSize -> Medium, PlotTheme -> "Detailed"], Plot[PDF[MarchenkoPasturDistribution[m/n], x], {x, 0, 1.8}, PlotTheme -> "Detailed", PlotLegends -> None, Exclusions -> None]]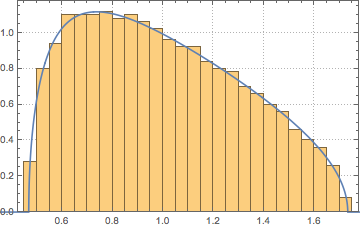

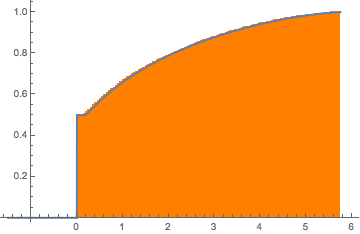
Out[4]=

For 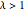, the Wishart matrix is singular. With probability 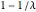, the distribution has a point mass at .

In[5]:=

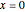m = 500; n = 2 m; CDF[MarchenkoPasturDistribution[n/m], 0]

Out[5]=

Generate a singular Wishart matrix with identity covariance and compute the scaled eigenvalues.

In[6]:=

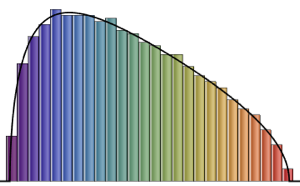
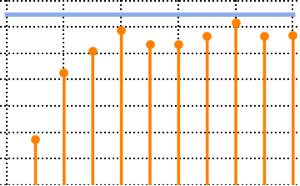
matrix = Transpose[#].# &[RandomVariate[NormalDistribution[], {m, n}]]; eigvs = Chop[Eigenvalues[matrix]/m];

There is a gap in the density of eigenvalues near 0, and the bin at 0 has a large density.

In[7]:=

Histogram[eigvs, {0.05}, PDF, PlotRange -> 1, ChartStyle -> Orange, ImageSize -> Medium]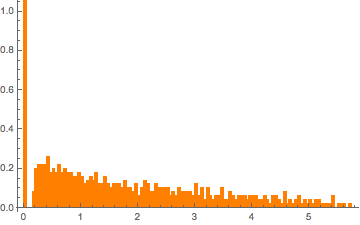

Out[7]=

Fit MarchenkoPasturDistribution to the eigenvalues.

In[8]:=

edist = EstimatedDistribution[eigvs, MarchenkoPasturDistribution[\[Lambda], 1]]

Out[8]=

CDF of the fitted distribution shows a jump discontinuity at the origin.

In[9]:=

Show[Histogram[eigvs, {0.05}, CDF, ChartStyle -> Orange], Quiet@Plot[CDF[edist, x], {x, -1.5, 5.75}, Exclusions -> None, PlotStyle -> Thick], ImageSize -> Medium, AxesOrigin -> {-1, 0}, PlotRange -> {{-1.5, 6}, {0, 1}}]

Out[9]=