マルチェンコ・パスツール分布
マルチェンコ・パスツール分布は,行列次元 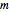 ,自由度
,自由度  (どちらも
(どちらも 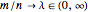 の割合で無限大になる傾向がある)のウィシャート行列の固有値の極限分布である.
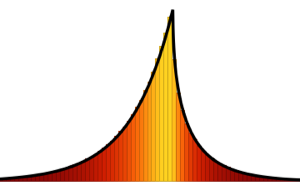
の割合で無限大になる傾向がある)のウィシャート行列の固有値の極限分布である.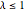 については,分布は質点を持たず,確率密度関数は明確に定義される.
については,分布は質点を持たず,確率密度関数は明確に定義される.
In[1]:=
PDF[MarchenkoPasturDistribution[1/2], x]Out[1]=
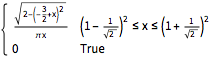
完全なWolfram言語入力を表示する
Out[2]=
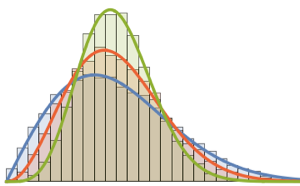
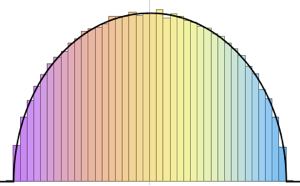
恒等尺度行列のあるウィシャート分布からサンプルを取り,スケールされた固有値を計算する.
In[3]:=

n = 10^4;
m = 10^3;
eigs = RandomVariate[
MatrixPropertyDistribution[Eigenvalues[x]/n,
x \[Distributed]
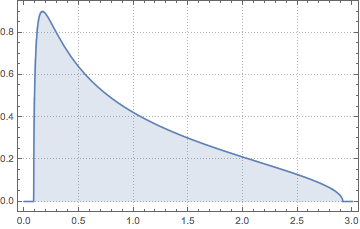
WishartMatrixDistribution[n, IdentityMatrix[m]]]];サンプルとして取られた結果をマルチェンコ・パスツール密度関数と比較する.
In[4]:=

Show[Histogram[eigs, {0.05}, "PDF", ImageSize -> Medium,
PlotTheme -> "Detailed"],
Plot[PDF[MarchenkoPasturDistribution[m/n], x], {x, 0, 1.8},
PlotTheme -> "Detailed", PlotLegends -> None, Exclusions -> None]]Out[4]=
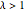 については,ウィシャート行列は特異行列である.確率
については,ウィシャート行列は特異行列である.確率 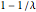 のとき,分布は
のとき,分布は 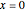 で質点を持つ.
で質点を持つ.
In[5]:=
m = 500; n = 2 m;
CDF[MarchenkoPasturDistribution[n/m], 0]Out[5]=
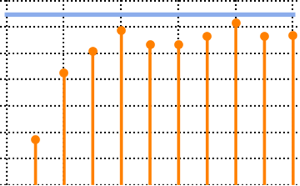
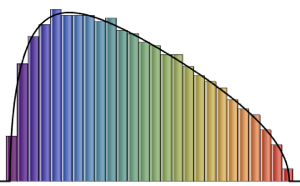
恒等共分散を持つ特異ウィシャート行列を生成し,スケールされた固有値を計算する.
In[6]:=
matrix = Transpose[#].# &[RandomVariate[NormalDistribution[], {m, n}]];
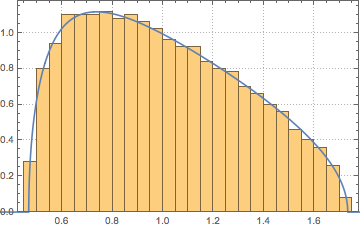
eigvs = Chop[Eigenvalues[matrix]/m];0付近で固有値の密度にギャップがあり,0のビンで密度が高くなっている.
In[7]:=
Histogram[eigvs, {0.05}, PDF, PlotRange -> 1, ChartStyle -> Orange,
ImageSize -> Medium]Out[7]=
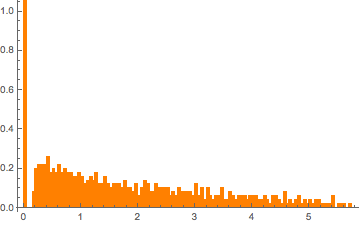
MarchenkoPasturDistributionを固有値にフィットする.
In[8]:=
edist = EstimatedDistribution[eigvs,
MarchenkoPasturDistribution[\[Lambda], 1]]Out[8]=
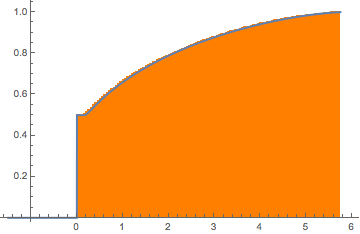
フィットされた分布の累積分布関数は,原点に不連続なジャンプがある.
完全なWolfram言語入力を表示する
Out[9]=