马尔琴科–巴斯德分布: Wolfram语言 11 的新功能

‹›

马尔琴科–巴斯德分布

马尔琴科–巴斯德分布是当矩阵维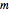度和自由度同时趋向于无穷且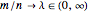时， Wishart 矩阵特征值的极限分布. 对于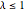，分布没有点质量，且概率密度函数是被明确定义的.

In[1]:=

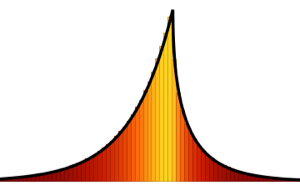
PDF[MarchenkoPasturDistribution[1/2], x]

Out[1]=

显示完整的 Wolfram 语言输入

In[2]:=

Plot[PDF[MarchenkoPasturDistribution[1/2], x], {x, 0, 3}, 
 PlotRange -> All, Exclusions -> None, Filling -> Axis, 
 PlotTheme -> "Detailed", ImageSize -> Medium, PlotLegends -> None]

Out[2]=

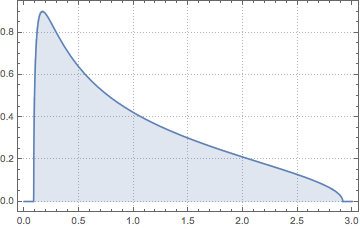
从具有单位尺度矩阵的 Wishart 分布采样，并计算缩放的特征值.

In[3]:=

n = 10^4;
m = 10^3;
eigs = RandomVariate[
   MatrixPropertyDistribution[Eigenvalues[x]/n, 
    x \[Distributed] 
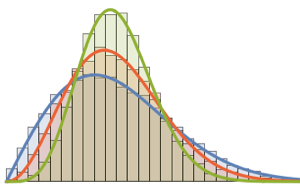
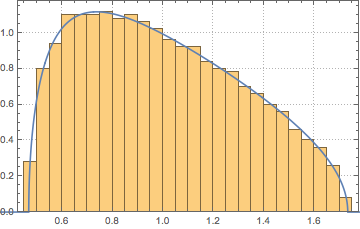
     WishartMatrixDistribution[n, IdentityMatrix[m]]]];

比较采样结果与马尔琴科–巴斯德密度函数.

In[4]:=

Show[Histogram[eigs, {0.05}, "PDF", ImageSize -> Medium, 
  PlotTheme -> "Detailed"], 
 Plot[PDF[MarchenkoPasturDistribution[m/n], x], {x, 0, 1.8}, 
  PlotTheme -> "Detailed", PlotLegends -> None, Exclusions -> None]]

Out[4]=

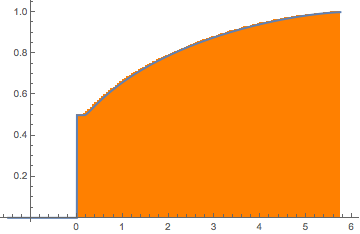
对于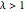，Wishart 矩阵是奇异的. 当概率为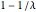时，分布在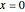处具有点质量.

In[5]:=

m = 500; n = 2 m;
 CDF[MarchenkoPasturDistribution[n/m], 0]

Out[5]=

生成具有单位协方差的奇异 Wishart 矩阵，并计算缩放的特征值.

In[6]:=

matrix = Transpose[#].# &[RandomVariate[NormalDistribution[], {m, n}]];
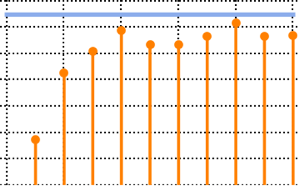
eigvs = Chop[Eigenvalues[matrix]/m];

在特征值密度接近于 0 处有一个空隙，并且箱在 0 具有较大的密度.

In[7]:=

Histogram[eigvs, {0.05}, PDF, PlotRange -> 1, ChartStyle -> Orange, 
 ImageSize -> Medium]

Out[7]=

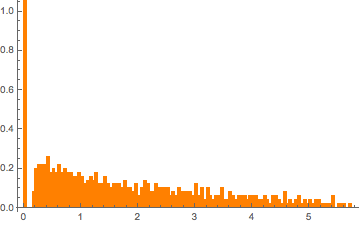
将 MarchenkoPasturDistribution 拟合到特征值.

In[8]:=

edist = EstimatedDistribution[eigvs, 
  MarchenkoPasturDistribution[\[Lambda], 1]]

Out[8]=

拟合分布的累积分布函数显示在原点有一个跳跃不连续点.

显示完整的 Wolfram 语言输入

In[9]:=

Show[Histogram[eigvs, {0.05}, CDF, ChartStyle -> Orange], 
 Quiet@Plot[CDF[edist, x], {x, -1.5, 5.75}, Exclusions -> None, 
   PlotStyle -> Thick], ImageSize -> Medium, AxesOrigin -> {-1, 0}, 
 PlotRange -> {{-1.5, 6}, {0, 1}}]

Out[9]=

Wolfram 语言™

马尔琴科–巴斯德分布

相关范例