Distribución de Marchenko–Pastur

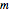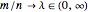La distribución de Marchenko–Pastur es la distribución de límite de valores propios de matrices de Wishart como la matriz de dimensión y grados de libertad , ambos tienden a infinito con relación . Para 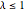, la distribución no tiene masa puntual y la función de densidad de probabilidad está bien definida.

In[1]:=

PDF[MarchenkoPasturDistribution[1/2], x]

Out[1]=

In[2]:=

Plot[PDF[MarchenkoPasturDistribution[1/2], x], {x, 0, 3}, PlotRange -> All, Exclusions -> None, Filling -> Axis, PlotTheme -> "Detailed", ImageSize -> Medium, PlotLegends -> None]

Out[2]=

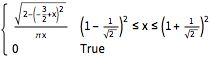
Tome una muestra de una distribución de Wishart con matriz de escala de identidad y calcule los valores propios escalados.

In[3]:=

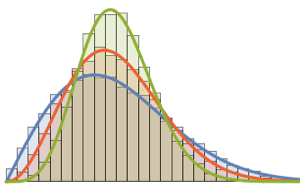
n = 10^4; m = 10^3; eigs = RandomVariate[ MatrixPropertyDistribution[Eigenvalues[x]/n, x \[Distributed] WishartMatrixDistribution[n, IdentityMatrix[m]]]];

Compare el resultado muestreado con la función de densidad de Marchenko–Pastur.

In[4]:=

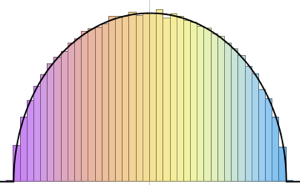
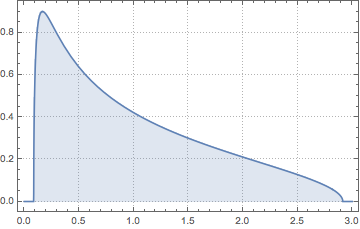
Show[Histogram[eigs, {0.05}, "PDF", ImageSize -> Medium, PlotTheme -> "Detailed"], Plot[PDF[MarchenkoPasturDistribution[m/n], x], {x, 0, 1.8}, PlotTheme -> "Detailed", PlotLegends -> None, Exclusions -> None]]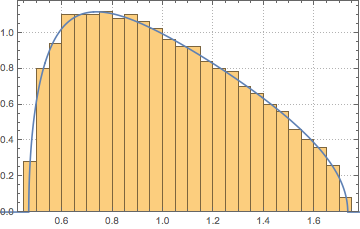

Out[4]=

Para 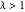, la matriz de Wishart es singular. Con probabilidad 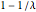, la distribución tiene una masa en el punto .

In[5]:=

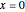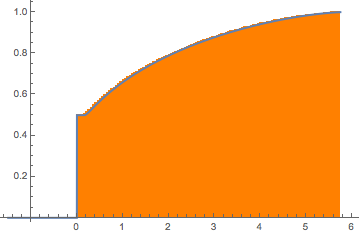
m = 500; n = 2 m; CDF[MarchenkoPasturDistribution[n/m], 0]

Out[5]=

Genere una matriz singular de Wishart con covarianza de identidad y calcule los valores propios escalados.

In[6]:=

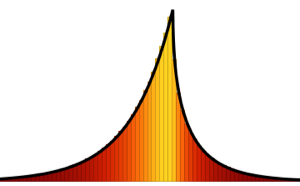
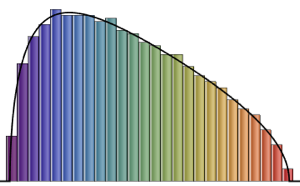
matrix = Transpose[#].# &[RandomVariate[NormalDistribution[], {m, n}]]; eigvs = Chop[Eigenvalues[matrix]/m];

Hay un vacío en la densidad de los valores propios cercanos a 0, y el contendedor 0 tiene una gran densidad.

In[7]:=

Histogram[eigvs, {0.05}, PDF, PlotRange -> 1, ChartStyle -> Orange, ImageSize -> Medium]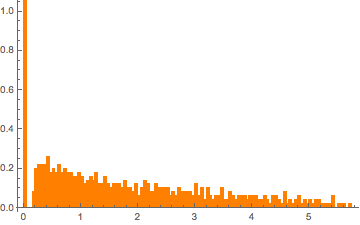

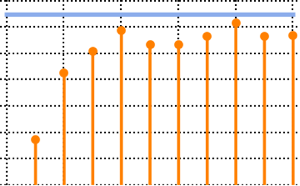
Out[7]=

Ajuste MarchenkoPasturDistribution a los valores propios.

In[8]:=

edist = EstimatedDistribution[eigvs, MarchenkoPasturDistribution[\[Lambda], 1]]

Out[8]=

La función de distribución de acumulación de la distribución ajustada muestra una discontinuidad de salto en el origen.

In[9]:=

Show[Histogram[eigvs, {0.05}, CDF, ChartStyle -> Orange], Quiet@Plot[CDF[edist, x], {x, -1.5, 5.75}, Exclusions -> None, PlotStyle -> Thick], ImageSize -> Medium, AxesOrigin -> {-1, 0}, PlotRange -> {{-1.5, 6}, {0, 1}}]

Out[9]=