Propiedades de distribuciones de matriz

La estadística de menor dimensión derivada de matrices aleatorias juegan roles significativos en la caracterización de conjuntos de matriz. En varias situaciones límites, las distribuciones de estas estadísticas colapsan en distintas clases de universalidad. MatrixPropertyDistribution proporciona un acceso conveniente para el muestreo y cálculo de la aproximación numérica de estas propiedades derivadas.

Tome una muestra de los dos valores propios mayores de un conjunto unitario de Gauss.

In[1]:=

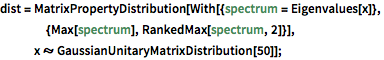
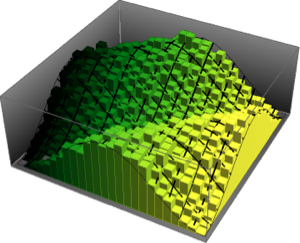
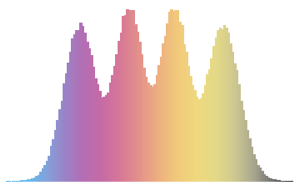
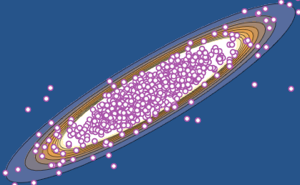
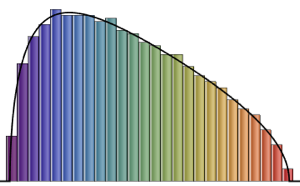
dist = MatrixPropertyDistribution[With[{spectrum = Eigenvalues[x]}, {Max[spectrum], RankedMax[spectrum, 2]}], x \[Distributed] GaussianUnitaryMatrixDistribution[50]];

In[2]:=

RandomVariate[dist]

Out[2]=

Visualice la distribución conjunta de los dos valores propios mayores con base en el resultado muestreado.

In[3]:=

sample = RandomVariate[dist, 10^4];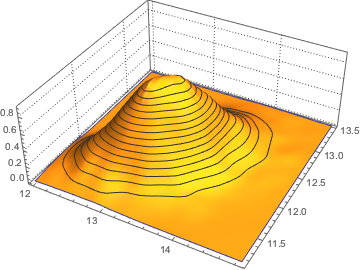

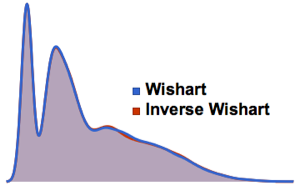
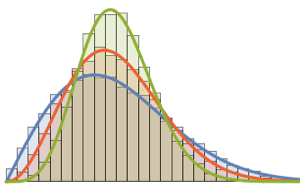
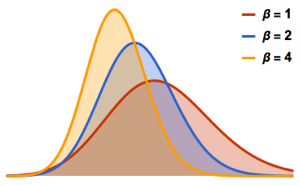
In[4]:=

SmoothHistogram3D[sample, "Scott", "PDF", PlotTheme -> "Detailed", ImageSize -> Medium]

Out[4]=

Tome una muestra del determinante de matrices de un conjunto ortogonal de Gauss y compare la distribución empírica con la expresión de forma cerrada.

In[5]:=

dist = MatrixPropertyDistribution[Det[x], x \[Distributed] GaussianOrthogonalMatrixDistribution[2]]; dets = RandomVariate[dist, 10^6];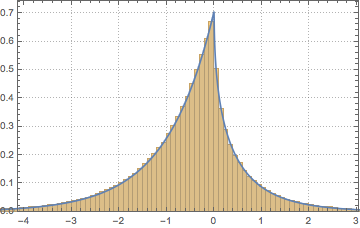

In[6]:=

empirical = Histogram[dets, {0.1}, PDF, PlotTheme -> "Detailed", ImageSize -> Medium]; detpdf[y_] := 1/Sqrt[2] Exp[ y] Piecewise[{{Erfc[Sqrt[2 y]], y >= 0}, {1, y < 0}}]; analytical = Plot[detpdf[y], {y, -5, 4}, Exclusions -> None, PlotLegends -> None, PlotTheme -> "Detailed", ImageSize -> Medium, Filling -> Axis]; Show[empirical, analytical]

Out[6]=

Aproxime el promedio del determinante por medio del método de Monte Carlo y compárelo con el valor actual.

In[7]:=

{N@Mean[dist], Integrate[x detpdf[x], {x, -Infinity, Infinity}]}

Out[7]=