Eigenschaften von Matrixverteilungen

Die von den Zufallsmatritzen abgeleiteten niedrigdimensionalen Statistiken spielen eine entscheidende Rolle bei der Charakterisierung der Matrixensembles. Für einige Grenzfällen kann man verschiedene Universalitätsklassen für die Verteilungen dieser Statistiken bestimmen. MatrixPropertyDistribution bietet einen bequemen Weg, die numerische Approximation dieser abgeleiteten Eigenschaften zu berechnen.

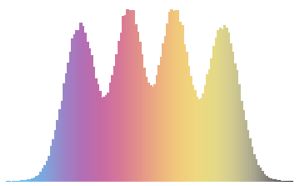
Nehmen Sie die zwei größten Eigenwerte eines Gaußschen unitären Ensembles.

In[1]:=

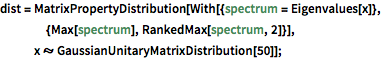
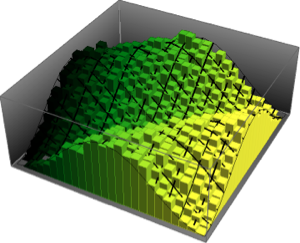
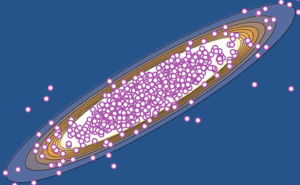
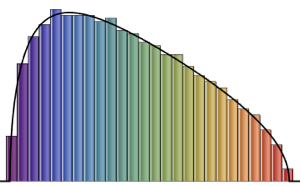
dist = MatrixPropertyDistribution[With[{spectrum = Eigenvalues[x]}, {Max[spectrum], RankedMax[spectrum, 2]}], x \[Distributed] GaussianUnitaryMatrixDistribution[50]];

In[2]:=

RandomVariate[dist]

Out[2]=

Visualisieren Sie die multivariate Verteilung der zwei größten Eigenwerte basierend auf dem Resultat.

In[3]:=

sample = RandomVariate[dist, 10^4];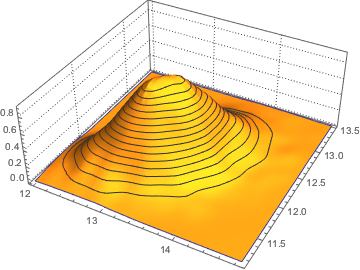

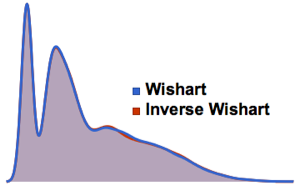
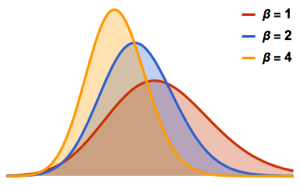
In[4]:=

SmoothHistogram3D[sample, "Scott", "PDF", PlotTheme -> "Detailed", ImageSize -> Medium]

Out[4]=

Nehmen Sie die Matritzendeterminante eines Gaußschen orthogonalen Ensembles und vergleichen Sie die empirische Verteilung mit dem geschlossenen Ausdruck.

In[5]:=

dist = MatrixPropertyDistribution[Det[x], x \[Distributed] GaussianOrthogonalMatrixDistribution[2]]; dets = RandomVariate[dist, 10^6];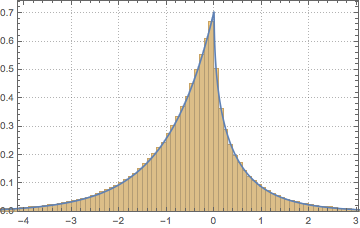

In[6]:=

empirical = Histogram[dets, {0.1}, PDF, PlotTheme -> "Detailed", ImageSize -> Medium]; detpdf[y_] := 1/Sqrt[2] Exp[ y] Piecewise[{{Erfc[Sqrt[2 y]], y >= 0}, {1, y < 0}}]; analytical = Plot[detpdf[y], {y, -5, 4}, Exclusions -> None, PlotLegends -> None, PlotTheme -> "Detailed", ImageSize -> Medium, Filling -> Axis]; Show[empirical, analytical]

Out[6]=

Approximieren Sie den Mittelwert der Determinante durch die Monte-Carlo-Methode und vergleichen Sie diesen mit dem tatsächlichen Wert.

In[7]:=

{N@Mean[dist], Integrate[x detpdf[x], {x, -Infinity, Infinity}]}

Out[7]=