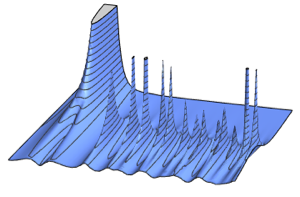
矩阵分布的属性: Wolfram语言 11 的新功能

矩阵分布的属性

来自随机矩阵的低维统计对表征矩阵系综起着重要的作用. 在各种极限情况下，这些统计量的分布归化成不同的普适类. MatrixPropertyDistribution 提供了对样本的方便接口，并计算这些派生属性的数值近似.

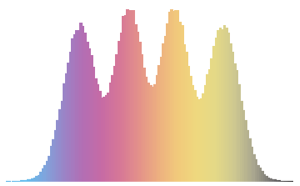
对来自高斯酉系综的最大的两个特征值进行采样.

In[1]:=

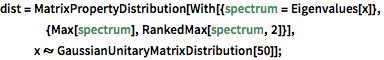
dist = MatrixPropertyDistribution[With[{spectrum = Eigenvalues[x]},
    {Max[spectrum], RankedMax[spectrum, 2]}], 
   x \[Distributed] GaussianUnitaryMatrixDistribution[50]];

In[2]:=

RandomVariate[dist]

Out[2]=

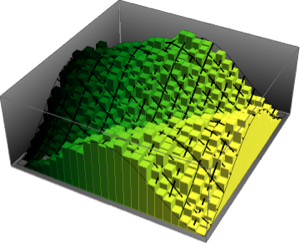
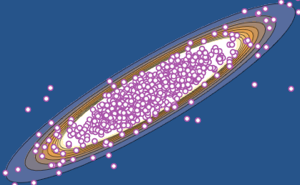
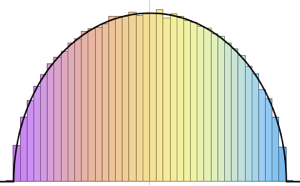
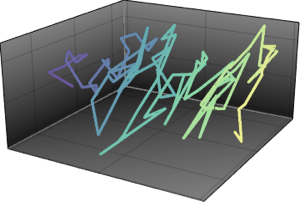
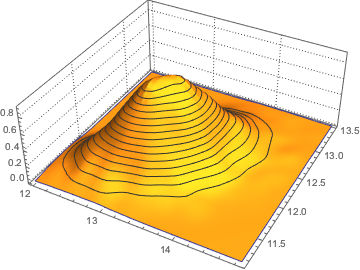
对基于采样结果的两个最大特征值的联合分布进行可视化.

In[3]:=

sample = RandomVariate[dist, 10^4];

显示完整的 Wolfram 语言输入

In[4]:=

SmoothHistogram3D[sample, "Scott", "PDF", PlotTheme -> "Detailed", 
 ImageSize -> Medium]

Out[4]=

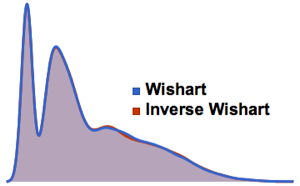
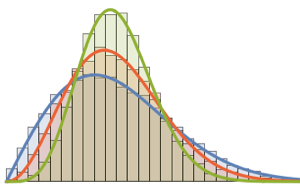
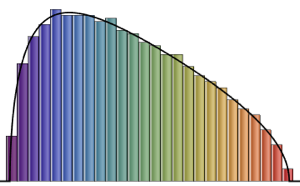
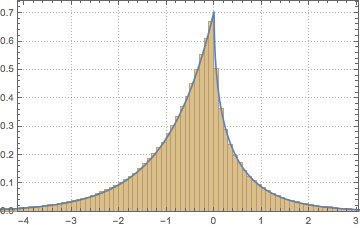
对来自高斯正交系综的矩阵行列式进行采样，并将经验分布与解析表达式比较.

In[5]:=

dist = MatrixPropertyDistribution[Det[x], 
   x \[Distributed] GaussianOrthogonalMatrixDistribution[2]];
dets = RandomVariate[dist, 10^6];

显示完整的 Wolfram 语言输入

In[6]:=

empirical = 
  Histogram[dets, {0.1}, PDF, PlotTheme -> "Detailed", 
   ImageSize -> Medium];
detpdf[y_] := 
  1/Sqrt[2] Exp[
    y] Piecewise[{{Erfc[Sqrt[2 y]], y >= 0}, {1, y < 0}}];
analytical = 
  Plot[detpdf[y], {y, -5, 4}, Exclusions -> None, 
   PlotLegends -> None, PlotTheme -> "Detailed", ImageSize -> Medium, 
   Filling -> Axis];
Show[empirical, analytical]

Out[6]=

通过蒙特卡罗抽样对行列式均值进行逼近，并与实际值比较.

In[7]:=

{N@Mean[dist], Integrate[x detpdf[x], {x, -Infinity, Infinity}]}

Out[7]=

Wolfram 语言™

矩阵分布的属性

相关范例