随机转动

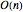CircularRealMatrixDistribution 表示维数为 的正交方阵的均匀分布，也称作正交群 的哈尔测度. 根据该分布生成的矩阵可以作为 -维向量空间中向量的转动算符.

通过由维数为 3 的 CircularRealMatrixDistribution 旋转固定的三维向量 (0,0,1) 得到随机向量，定义它的分布.

In[1]:=

\[ScriptCapitalD] = MatrixPropertyDistribution[r.{0, 0, 1}, r \[Distributed] CircularRealMatrixDistribution[3]];

使用该分布在单位球面上对点进行采样.

In[2]:=

points = RandomVariate[\[ScriptCapitalD], 10^3];

检查是否所有采样点属于单位球.

In[3]:=

AllTrue[points, RegionMember[Sphere[3]]]

Out[3]=

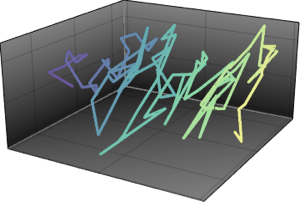
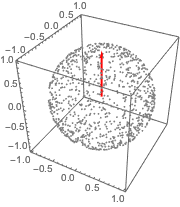
绘制采样点与原始向量.

In[4]:=

Graphics3D[{{Gray, PointSize[Small], Point[points]}, {Red, Thick, Arrow[{{0, 0, 0}, {0, 0, 1}}]}}, Axes -> True]

Out[4]=

柱面坐标下球面面积元由 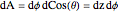给出.

In[5]:=

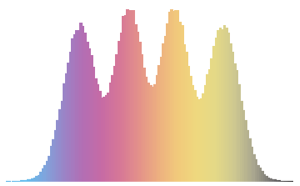
{x, y, z} = Transpose[points]; \[Phi] = ArcTan[y/x];

检查 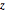和 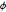的边缘分布是否均匀.

In[6]:=

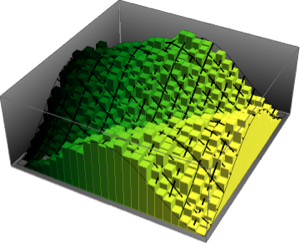
Histogram[#, 20, PDF] & /@ {\[Phi], z}

Out[6]=

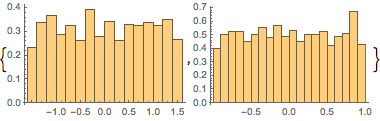
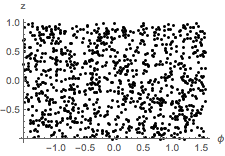
通过检查 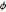和 的联合分布是否为均匀分布，检查采样点是否在球表面上均匀分布.

In[7]:=

Graphics[Point[Transpose[{\[Phi], z}]], Axes -> True, AxesOrigin -> {-\[Pi]/2, -1}, AxesLabel -> {"\[Phi]", "z"}]

Out[7]=

检验 和 的联合分布为均匀分布的假设.

In[8]:=

DistributionFitTest[Transpose[{\[Phi], z}], UniformDistribution[{{-Pi/2, Pi/2}, {-1, 1}}], "TestConclusion"]

Out[8]=