Rotations aléatoires

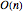CircularRealMatrixDistribution représente une loi uniforme des matrices carrées orthogonales de dimension , également connue sous le nom de la mesure de Haar sur le groupe orthogonal . Les matrices générées selon cette loi peuvent agir comme opérateurs pour les vecteurs de rotation dans un espace vectoriel de dimension.

Définissez la distribution des vecteurs aléatoires obtenus par rotation d'un vecteur en 3D fixe (0,0,1) par une matrice aléatoire à partir de CircularRealMatrixDistribution de dimension 3.

In[1]:=

\[ScriptCapitalD] = MatrixPropertyDistribution[r.{0, 0, 1}, r \[Distributed] CircularRealMatrixDistribution[3]];

Utilisez cette distribution pour échantillonner des points sur la surface de la sphère unitaire.

In[2]:=

points = RandomVariate[\[ScriptCapitalD], 10^3];

Vérifiez si tous les points d'échantillonnage appartiennent à l'unité de sphère.

In[3]:=

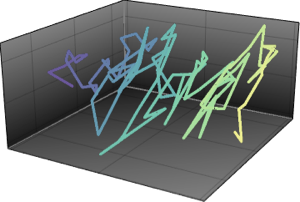
AllTrue[points, RegionMember[Sphere[3]]]

Out[3]=

Tracez les points d'échantillonnage avec le vecteur original.

In[4]:=

Graphics3D[{{Gray, PointSize[Small], Point[points]}, {Red, Thick, Arrow[{{0, 0, 0}, {0, 0, 1}}]}}, Axes -> True]

Out[4]=

L'élément de surface sur la sphère en coordonnées cylindriques est donnée par .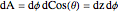

In[5]:=

{x, y, z} = Transpose[points]; \[Phi] = ArcTan[y/x];

Vérifiez que les distributions marginales de 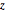et 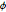sont uniformes.

In[6]:=

Histogram[#, 20, PDF] & /@ {\[Phi], z}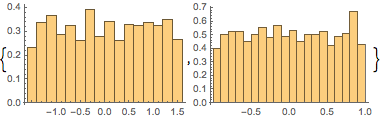

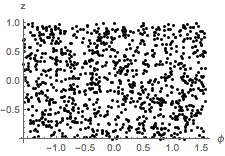
Out[6]=

Vérifiez si les points d'échantillonnage sont distribués uniformément sur la surface de la sphère en vérifiant que la distribution conjointe de 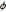et 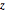est uniforme.

In[7]:=

Graphics[Point[Transpose[{\[Phi], z}]], Axes -> True, AxesOrigin -> {-\[Pi]/2, -1}, AxesLabel -> {"\[Phi]", "z"}]

Out[7]=

Testez l'hypothèse que la distribution conjointe 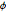de et de 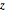est uniforme.

In[8]:=

DistributionFitTest[Transpose[{\[Phi], z}], UniformDistribution[{{-Pi/2, Pi/2}, {-1, 1}}], "TestConclusion"]

Out[8]=