Rotações aleatórias

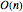CircularRealMatrixDistribution representa uma distribuição uniforme das matrizes quadradas ortogonais de dimensão , também conhecida como a medida de Haar no grupo ortogonal . As matrizes geradas de acordo com essa distribuição podem atuar como operadores de rotação para vetores em um espaço vetorial -dimensional.

Defina uma distribuição de vetores aleatórios obtidos com a rotação de um vetor em 3D fixo (0,0,1) por uma matriz aleatória de CircularRealMatrixDistribution de dimensão 3.

In[1]:=

\[ScriptCapitalD] = MatrixPropertyDistribution[r.{0, 0, 1}, r \[Distributed] CircularRealMatrixDistribution[3]];

Use esta distribuição para fazer uma amostra de pontos na área de superfície da esfera.

In[2]:=

points = RandomVariate[\[ScriptCapitalD], 10^3];

Verifique se todos os pontos da amostra pertencem à unidade da esfera.

In[3]:=

AllTrue[points, RegionMember[Sphere[3]]]

Out[3]=

Represente graficamente os pontos da amostra com o vetor original.

In[4]:=

Graphics3D[{{Gray, PointSize[Small], Point[points]}, {Red, Thick, Arrow[{{0, 0, 0}, {0, 0, 1}}]}}, Axes -> True]

Out[4]=

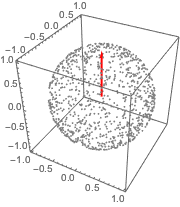
O elemento da área de superfície da esfera em coordenadas cilíndricas é dado por .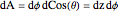

In[5]:=

{x, y, z} = Transpose[points]; \[Phi] = ArcTan[y/x];

Verifique se as distribuições marginais d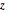e e 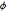são uniformes.

In[6]:=

Histogram[#, 20, PDF] & /@ {\[Phi], z}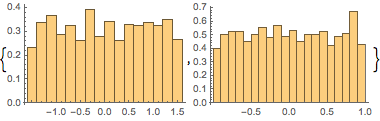

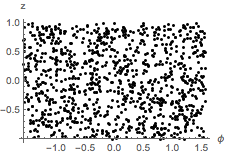
Out[6]=

Verifique se os pontos da amostra estão distribuídos uniformemente na superfície da esfera verificando se a distribuição conjunta de 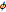e é 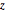uniforme.

In[7]:=

Graphics[Point[Transpose[{\[Phi], z}]], Axes -> True, AxesOrigin -> {-\[Pi]/2, -1}, AxesLabel -> {"\[Phi]", "z"}]

Out[7]=

Teste a hipótese de que a distribuição conjunta de 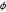e é 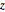uniforme.

In[8]:=

DistributionFitTest[Transpose[{\[Phi], z}], UniformDistribution[{{-Pi/2, Pi/2}, {-1, 1}}], "TestConclusion"]

Out[8]=