Wolfram Language™

Zufallsrotationen

CircularRealMatrixDistribution repräsentiert eine Gleichverteilung der orthogonalen Matrix der Dimension n, auch bekannt als das Haarsche Maß auf der orthogonalen Gruppe 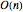. Die entsprechend dieser Verteilung generierten Matritzen können Drehoperatoren für Vektoren im -dimensionalen Vektorraum sein.

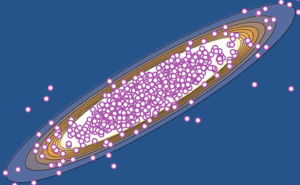
Bestimmen Sie eine Verteilung von Zufallsvektoren, die durch Drehung eines fixierten 3D-Vektors (0,0,1) durch eine Zufallsmatrix aus CircularRealMatrixDistribution der dritten Dimension ermittelt werden.

In[1]:=

\[ScriptCapitalD] = MatrixPropertyDistribution[r.{0, 0, 1}, r \[Distributed] CircularRealMatrixDistribution[3]];

Verwenden Sie die Verteilung, um eine Stichprobe von Punkten auf der Oberfläche der Einheitskugel zu nehmen.

In[2]:=

points = RandomVariate[\[ScriptCapitalD], 10^3];

Überprüfen Sie, ob alle Punkte zur Einheitskugel gehören.

In[3]:=

AllTrue[points, RegionMember[Sphere[3]]]

Out[3]=

Plotten Sie die Punkte mit dem ursprünglichen Vektor.

In[4]:=

Graphics3D[{{Gray, PointSize[Small], Point[points]}, {Red, Thick, Arrow[{{0, 0, 0}, {0, 0, 1}}]}}, Axes -> True]

Out[4]=

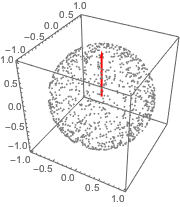
Das Element des Flächeninhalts der Kugeloberfläche in Zylinderkoordinaten ist gegeben durch .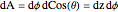

In[5]:=

{x, y, z} = Transpose[points]; \[Phi] = ArcTan[y/x];

Überprüfen Sie, ob die Randverteilungen 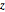und 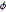gleichverteilt sind.

In[6]:=

Histogram[#, 20, PDF] & /@ {\[Phi], z}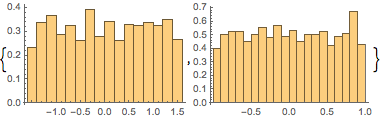

Out[6]=

Überprüfen Sie, ob die Punkte auf der Kugeloberfläche gleichverteilt sind, indem Sie ermitteln, ob es sich bei der multivariaten Verteilung von 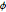und 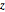um eine Gleichverteilung handelt.

In[7]:=

Graphics[Point[Transpose[{\[Phi], z}]], Axes -> True, AxesOrigin -> {-\[Pi]/2, -1}, AxesLabel -> {"\[Phi]", "z"}]

Out[7]=

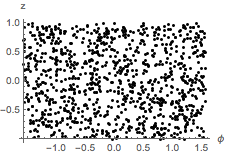
Testen Sie die Hypothese, dass die multivariate Verteilung von 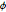und 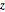die gleichen Randverteilungen hat.

In[8]:=

DistributionFitTest[Transpose[{\[Phi], z}], UniformDistribution[{{-Pi/2, Pi/2}, {-1, 1}}], "TestConclusion"]

Out[8]=