ランダム回転: Wolfram言語 11の新機能

ランダム回転

CircularRealMatrixDistributionは，直交群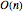についてのハール(Harr)測度としても知られる，次元の直交平方行列の一様分布を表す．この分布に従って生成された行列は，次元ベクトル空間内のベクトルについての回転演算子として作用する．

次元3のCircularRealMatrixDistributionからのランダム行列によって，固定3Dベクトル(0,0,1)を回転させることで得られたランダムベクトルの分布を定義する．

In[1]:=

\[ScriptCapitalD] = 
  MatrixPropertyDistribution[r.{0, 0, 1}, 
   r \[Distributed] CircularRealMatrixDistribution[3]];

この分布を使って単位球面上の点をサンプルとして取る．

In[2]:=

points = RandomVariate[\[ScriptCapitalD], 10^3];

サンプル点のすべてが単位球面に属すかどうかをチェックする．

In[3]:=

AllTrue[points, RegionMember[Sphere[3]]]

Out[3]=

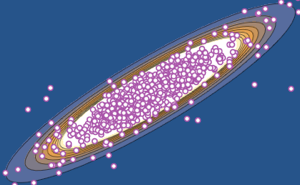
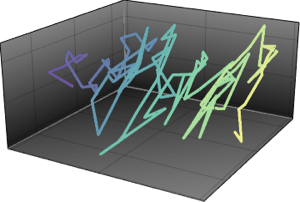
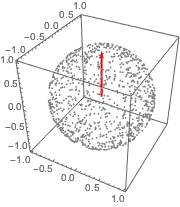
サンプル点をもとのベクトルとともにプロットする．

完全なWolfram言語入力を表示する

In[4]:=

Graphics3D[{{Gray, PointSize[Small], Point[points]}, {Red, Thick, 
   Arrow[{{0, 0, 0}, {0, 0, 1}}]}}, Axes -> True]

Out[4]=

円柱座標における球の表面の要素は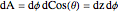で与えられる．

In[5]:=

{x, y, z} = Transpose[points];
\[Phi] = ArcTan[y/x];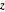

と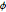の周辺分布が一様かどうかをチェックする．

In[6]:=

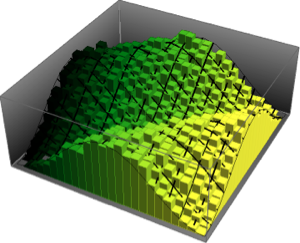
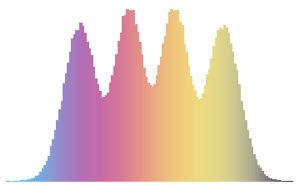
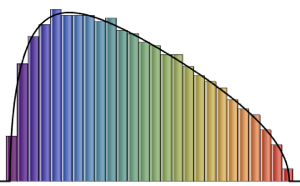
Histogram[#, 20, PDF] & /@ {\[Phi], z}

Out[6]=

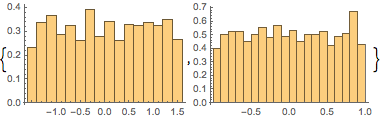
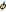との結合分布が一様かどうかをチェックすることで，サンプル点が球面上で一様に分布しているかどうかをチェックする．

完全なWolfram言語入力を表示する

In[7]:=

Graphics[Point[Transpose[{\[Phi], z}]], Axes -> True, 
 AxesOrigin -> {-\[Pi]/2, -1}, AxesLabel -> {"\[Phi]", "z"}]

Out[7]=

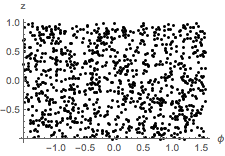
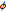と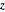の結合分布が一様であるという仮説を検定する．

In[8]:=

DistributionFitTest[Transpose[{\[Phi], z}], 
 UniformDistribution[{{-Pi/2, Pi/2}, {-1, 1}}], "TestConclusion"]

Out[8]=