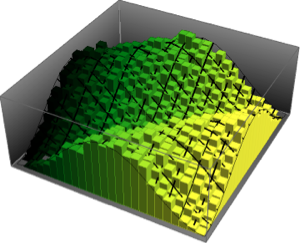
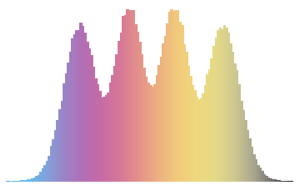
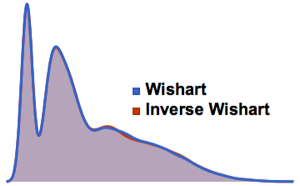
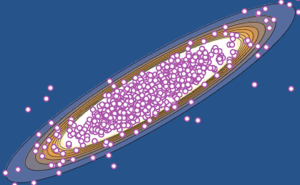
벡터 자기 회귀 과정의 시뮬레이션
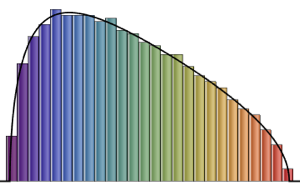
MatrixNormalDistribution을 사용하여 벡터 자기 회귀 과정의 시뮬레이션을 실시합니다.
In[1]:=
sigR = Covariance[ARProcess[{a}, 1][Range[0, 100]]];
sigC = {{s11, s12}, {s12, s22}};In[2]:=
rules = {a -> 1/2, s11 -> 1, s12 -> 1/2, s22 -> 3};In[3]:=
\[ScriptCapitalD] = MatrixNormalDistribution[sigR, sigC] /. rules;행렬 분포에서 랜덤 샘플 시뮬레이션을 실시합니다.
In[4]:=
vals = RandomVariate[\[ScriptCapitalD], 10^4];샘플 된 값으로 TemporalData를 구축합니다.
In[5]:=
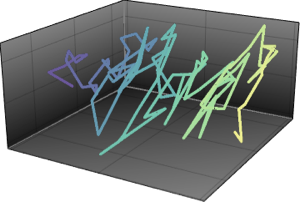
td = TemporalData[vals, {0, Length[sigR] - 1, 1},
ValueDimensions -> 2]Out[5]=
대각선 벡터 자기 회귀 과정을 추정합니다.
In[6]:=
proc = ARProcess[{a IdentityMatrix[2]}, sigC];In[7]:=
sol = FindProcessParameters[td, proc]Out[7]=
오리지널 값과 비교합니다.
In[8]:=
sol[[All, 2]] - rules[[All, 2]]Out[8]=