최장 증가 부분 문자열
최장 증가 부분 문자열이 최대 길이  인
인 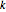 개의 본래 대체수 ℐ(k,n)은,
개의 본래 대체수 ℐ(k,n)은, ![]() 로 평균하여 계산할 수있습니다.
로 평균하여 계산할 수있습니다. 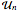 는 CircularUnitaryMatrixDistribution에서 끌어온 차원
는 CircularUnitaryMatrixDistribution에서 끌어온 차원  의 행렬입니다.
의 행렬입니다.
In[1]:=
{k, n} = {6, 2};행렬의 특성 분포를 정의하고 평균을 계산합니다.
In[2]:=

\[ScriptCapitalD] =
MatrixPropertyDistribution[Abs[Tr[\[ScriptCapitalU]]]^(
2 k), \[ScriptCapitalU] \[Distributed]
CircularUnitaryMatrixDistribution[n]];
N[Mean[\[ScriptCapitalD]]]Out[2]=
직접 숫자와 비교합니다.
In[3]:=
Count[Permutations[Range[k]],
perm_ /; Length[LongestOrderedSequence[perm]] <= n]Out[3]=
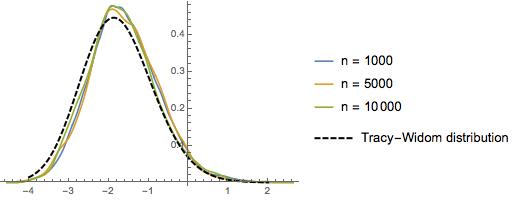
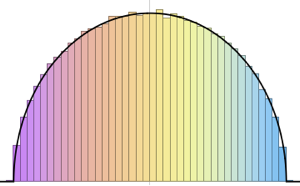
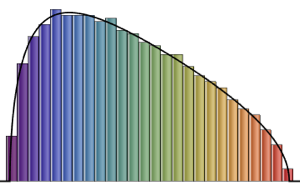
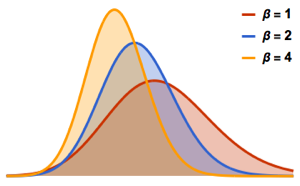
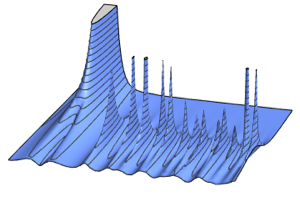
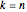 일때, 임의 치환의 최대 증가 부분열의 스케일된 길이의 분포는
일때, 임의 치환의 최대 증가 부분열의 스케일된 길이의 분포는 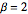 의 Tracy–Widom 분포에 수렴합니다.
의 Tracy–Widom 분포에 수렴합니다.
In[4]:=

sample[n_] :=
1/n^(1/6) (Table[
Length[LongestOrderedSequence[
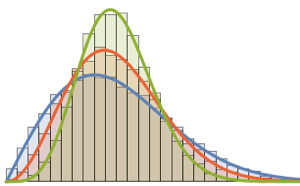
RandomSample[Range[n]]]], {2000}] - 2.0 Sqrt[n]);차원의 증가에 대한 샘플로 주어진 스케일된 길이의 매끄러운 히스토그램을 Tracy–Widom 분포의 확률 밀도 함수와 비교합니다.
전체 Wolfram 언어 입력 표시하기
Out[5]=