Marchenko–Pastur 분포
Marchenko–Pastur 분포는 행렬 차원  , 그리고 자유도
, 그리고 자유도  , 둘다
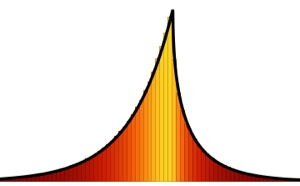
, 둘다  의 비율의 무한대 경향을 가진 위샤트 행렬의 고유값의 극한 분포입니다.
의 비율의 무한대 경향을 가진 위샤트 행렬의 고유값의 극한 분포입니다.  에 대해 분포는 질점을 가지지않으며 확률 밀도 함수는 명확하게 정의됩니다.
에 대해 분포는 질점을 가지지않으며 확률 밀도 함수는 명확하게 정의됩니다.
In[1]:=
PDF[MarchenkoPasturDistribution[1/2], x]Out[1]=

전체 Wolfram 언어 입력 표시하기
Out[2]=

항등 척도 행렬이있는 위샤트 분포에서 샘플을 채취하고 스케일된 고유값을 계산합니다.
In[3]:=

n = 10^4;
m = 10^3;
eigs = RandomVariate[
MatrixPropertyDistribution[Eigenvalues[x]/n,
x \[Distributed]
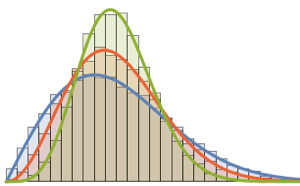
WishartMatrixDistribution[n, IdentityMatrix[m]]]];샘플된 결과를 Marchenko–Pastur 밀도 함수와 비교합니다.
In[4]:=

Show[Histogram[eigs, {0.05}, "PDF", ImageSize -> Medium,
PlotTheme -> "Detailed"],
Plot[PDF[MarchenkoPasturDistribution[m/n], x], {x, 0, 1.8},
PlotTheme -> "Detailed", PlotLegends -> None, Exclusions -> None]]Out[4]=

 에대해 위샤트 행렬은 특이 행렬입니다. 확률
에대해 위샤트 행렬은 특이 행렬입니다. 확률  의 경우, 분포는
의 경우, 분포는  에서 질점을 가집니다.
에서 질점을 가집니다.
In[5]:=
m = 500; n = 2 m;
CDF[MarchenkoPasturDistribution[n/m], 0]Out[5]=
항등 공분산을 가지는 특이 위샤트 행렬을 생성하고 스케일 된 고유값을 계산합니다.
In[6]:=
matrix = Transpose[#].# &[RandomVariate[NormalDistribution[], {m, n}]];
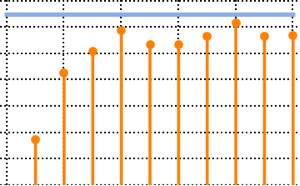
eigvs = Chop[Eigenvalues[matrix]/m];0 부근에서 고유값의 밀도에 차이가 있고, 0의 빈에서 밀도가 높아지고 있습니다.
In[7]:=
Histogram[eigvs, {0.05}, PDF, PlotRange -> 1, ChartStyle -> Orange,
ImageSize -> Medium]Out[7]=

MarchenkoPasturDistribution을 고유값에 맞춥니다.
In[8]:=
edist = EstimatedDistribution[eigvs,
MarchenkoPasturDistribution[\[Lambda], 1]]Out[8]=
적합된 분포의 누적 분포 함수는 원점의 불연속 점프를 보입니다.
전체 Wolfram 언어 입력 표시하기
Out[9]=