행렬의 스펙트럼 밀도
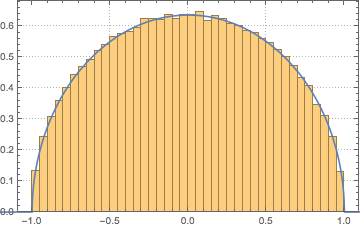
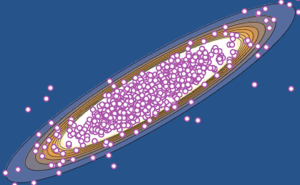
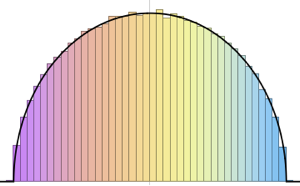
많은 행렬 분포의 스펙트럼 밀도는 상응하는 일반적인 극한 모양을 가집니다. 독립항을 포함하는 해밀턴 랜덤 행렬의 경우 위그너 반원 법칙을 따릅니다.
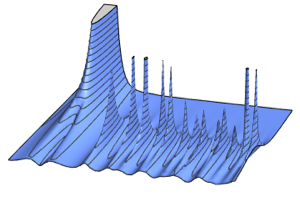
가우시안 앙상블의 행렬의 스케일된 스펙트럼 밀도는 양자 조화 진동자의 고유 함수와 관련된 유한 행렬 차원에 대해 닫힘식을 갖습니다.
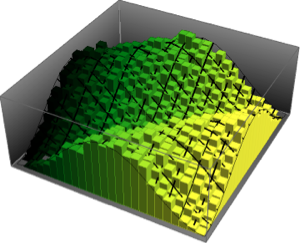
스케일된 가우시안 유니타리 앙상블의 스펙트럼을 나타내고 이 결합 스펙트럼 밀도의 닫힘식의 표현을 제공하기 위해 이 MatrixPropertyDistribution을 사용합니다.
In[1]:=

scaledSpectrum\[ScriptCapitalD][n_] :=
MatrixPropertyDistribution[
Eigenvalues[\[Lambda]]/(2 Sqrt[n]), \[Lambda] \[Distributed]
GaussianUnitaryMatrixDistribution[n]];In[2]:=
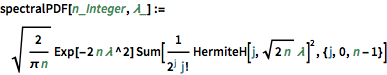
spectralPDF[n_Integer, \[Lambda]_] :=
Sqrt[2/(\[Pi] n)]
Exp[-2 n \[Lambda]^2] Sum[
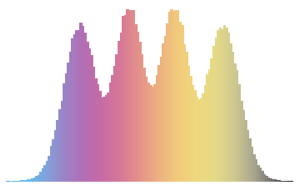
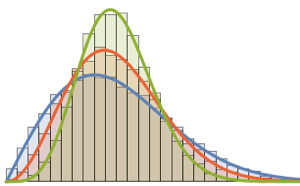
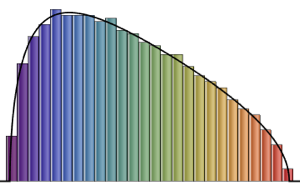
1/(2^j j!) HermiteH[j, Sqrt[2 n] \[Lambda]]^2, {j, 0, n - 1}]밀도 극대치의 수가 행렬 크기와 동일한 차원이 낮은 행렬에는 특징적인 진동 패턴이 보입니다.
In[3]:=
scaledSpectra =
Flatten[RandomVariate[scaledSpectrum\[ScriptCapitalD][#],
10^5]] & /@ {3, 4, 5};전체 Wolfram 언어 입력 표시하기
Out[4]=
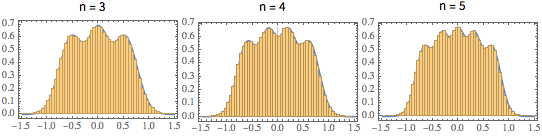
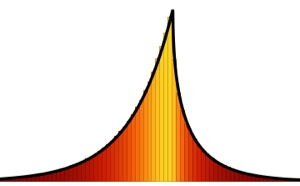
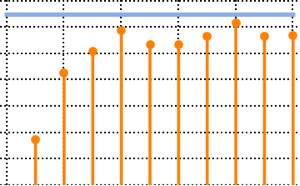
차원이 높은 극한에서, 밀도는 WignerSemicircleDistribution에 수렴합니다.
In[5]:=
n = 250;
scaledSpectrum =
Flatten[RandomVariate[scaledSpectrum\[ScriptCapitalD][n], 10^2]];전체 Wolfram 언어 입력 표시하기
Out[6]=