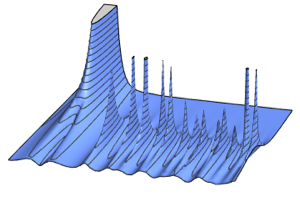
행렬 분포의 특성
랜덤 행렬로부터 유도된 저차원 통계는 매트릭스 앙상블의 특성 결정에 중요한 역할을 합니다. 여러가지 극한 상황에서 이러한 통계 분포는 다양한 보편성 클래스에 분해됩니다. MatrixPropertyDistribution은 이러한 파생 매개 변수의 수치적 근사의 샘플링과 계산에 편리한 접근을 제공합니다.
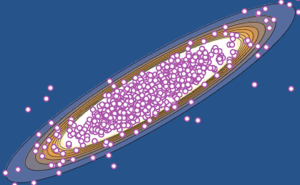
가우시안 유니타리 앙상블에서 가장 큰 두개의 고유값을 샘플링합니다.
In[1]:=
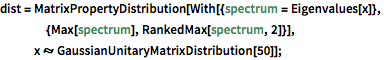
dist = MatrixPropertyDistribution[With[{spectrum = Eigenvalues[x]},
{Max[spectrum], RankedMax[spectrum, 2]}],
x \[Distributed] GaussianUnitaryMatrixDistribution[50]];In[2]:=
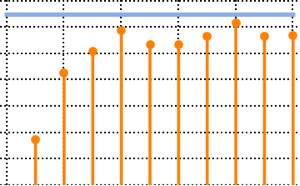
RandomVariate[dist]Out[2]=
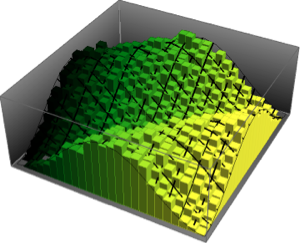
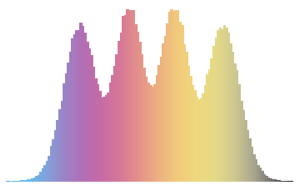
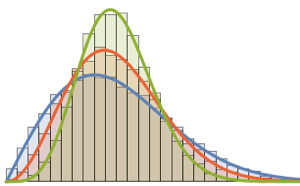
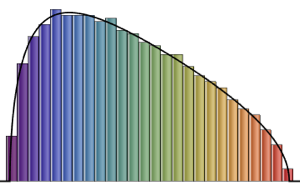
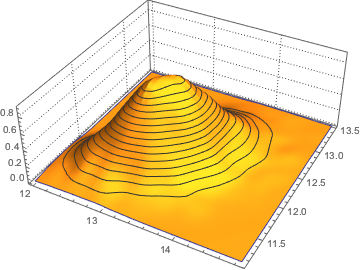
두개의 가장 큰 고유값의 결합 분포를 샘플된 결과를 바탕으로 시각화합니다.
In[3]:=
sample = RandomVariate[dist, 10^4];전체 Wolfram 언어 입력 표시하기
Out[4]=
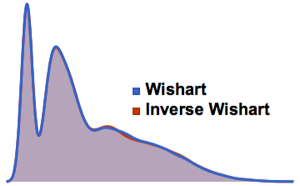
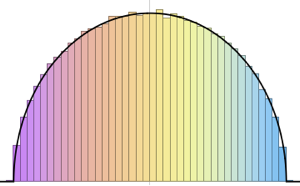
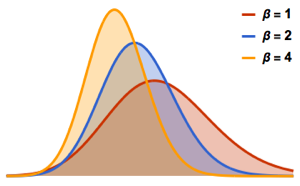
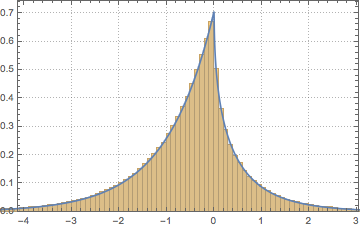
가우시안 직교 앙상블의 행렬식을 샘플링하고 경험 분포와 닫힘식 표현식을 비교합니다.
In[5]:=

dist = MatrixPropertyDistribution[Det[x],
x \[Distributed] GaussianOrthogonalMatrixDistribution[2]];
dets = RandomVariate[dist, 10^6];전체 Wolfram 언어 입력 표시하기
Out[6]=
행렬식의 평균을 몬테카를로 샘플링으로 근사하고 실제값과 비교합니다.
In[7]:=
{N@Mean[dist], Integrate[x detpdf[x], {x, -Infinity, Infinity}]}Out[7]=