램덤 회전
CircularRealMatrixDistribution은 직교 그룹 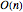 에 대한 하르 (Harr) 측도라고도 알려져 있는 차원 n의 직교 평방 행렬의 균일한 분포를 나타냅니다. 이 분포로 생성된 행렬은
에 대한 하르 (Harr) 측도라고도 알려져 있는 차원 n의 직교 평방 행렬의 균일한 분포를 나타냅니다. 이 분포로 생성된 행렬은  -차원 벡터 공간에서 벡터에 대한 회전 연산자로 작용합니다.
-차원 벡터 공간에서 벡터에 대한 회전 연산자로 작용합니다.
차원 3의 CircularRealMatrixDistribution에서 랜덤 행렬에의해 고정 3D 벡터 (0,0,1)를 회전 시킴으로써 얻어진 랜덤 벡터의 분포를 정의합니다.
In[1]:=
\[ScriptCapitalD] =
MatrixPropertyDistribution[r.{0, 0, 1},
r \[Distributed] CircularRealMatrixDistribution[3]];이 분포를 사용하여 단위 구면상의 점을 샘플합니다.
In[2]:=
points = RandomVariate[\[ScriptCapitalD], 10^3];샘플 점의 모든 단위 공에 위치하는지 여부를 체크합니다.
In[3]:=
AllTrue[points, RegionMember[Sphere[3]]]Out[3]=
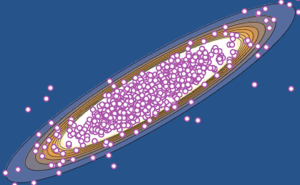
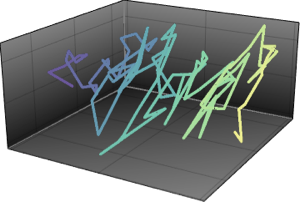
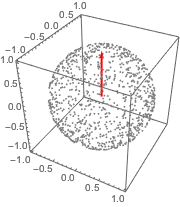
샘플 점을 오리지널 벡터와 함께 플롯합니다.
전체 Wolfram 언어 입력 표시하기
Out[4]=
원주 좌표의 공의 표면 요소는 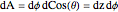 에서 주어집니다.
에서 주어집니다.
In[5]:=
{x, y, z} = Transpose[points];
\[Phi] = ArcTan[y/x];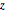 와
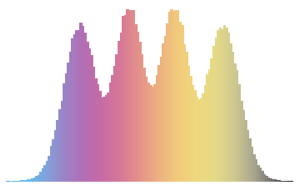
와 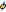 주변 분포가 균일한지 여부를 체크합니다.
주변 분포가 균일한지 여부를 체크합니다.
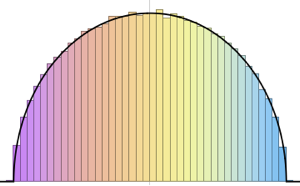
In[6]:=
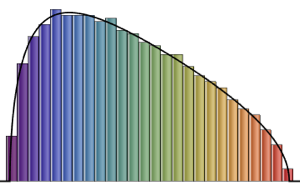
Histogram[#, 20, PDF] & /@ {\[Phi], z}Out[6]=
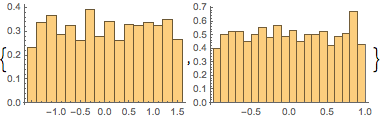
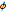 와
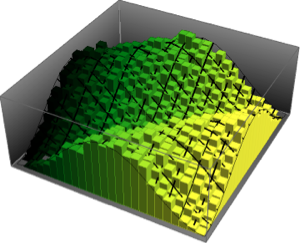
와 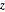 의 결합 분포의 균일 여부를 확인하여 샘플 점이 구면에서 균일하게 분포되어 있는지를 체크합니다.
의 결합 분포의 균일 여부를 확인하여 샘플 점이 구면에서 균일하게 분포되어 있는지를 체크합니다.
전체 Wolfram 언어 입력 표시하기
Out[7]=
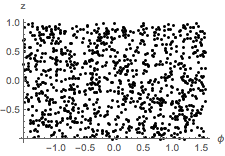
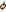 와
와 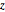 의 결합 분포가 균일하다는 가설을 검정합니다.
의 결합 분포가 균일하다는 가설을 검정합니다.
In[8]:=
DistributionFitTest[Transpose[{\[Phi], z}],
UniformDistribution[{{-Pi/2, Pi/2}, {-1, 1}}], "TestConclusion"]Out[8]=