가우시안 분포의 고유값 간격

행렬 분포의 고유값의 간격 (연속 고유 값의 차분)은 중원자의 에너지 준위 간격 등 자연의 수많은 시스템에서 볼 수있는 보편적인 극한 형태를 가집니다.

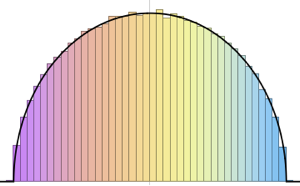
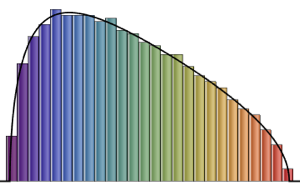
다양한 가우스 앙상블에서 2×2 행렬의 고유값 간격을 샘플링합니다.

In[1]:=

gaussiandists = {GaussianOrthogonalMatrixDistribution[2], GaussianUnitaryMatrixDistribution[2], GaussianSymplecticMatrixDistribution[2]};

In[2]:=

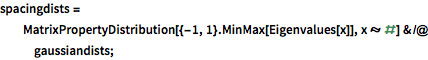
spacingdists = MatrixPropertyDistribution[{-1, 1}.MinMax[Eigenvalues[x]], x \[Distributed] #] & /@ gaussiandists;

In[3]:=

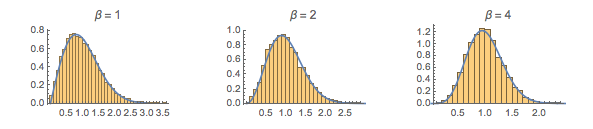
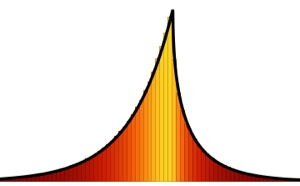
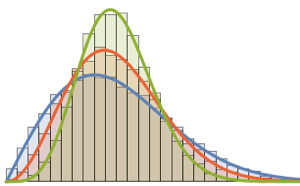
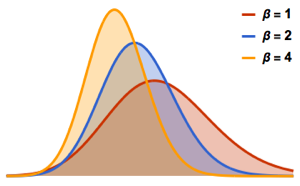
gaps = Normalize[RandomVariate[#, 10000], Mean] & /@ spacingdists;

각 분포의 히스토그램을 Dyson 지수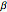가 1,2,4의 경우 Wigner 추측으로 알려진 각 닫힘 형식과 비교합니다.

In[4]:=

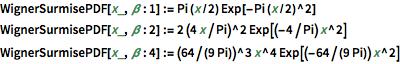
WignerSurmisePDF[x_, \[Beta] : 1] := Pi (x/2) Exp[-Pi (x/2)^2] WignerSurmisePDF[x_, \[Beta] : 2] := 2 (4 x/Pi)^2 Exp[(-4/Pi) x^2] WignerSurmisePDF[ x_, \[Beta] : 4] := (64/(9 Pi))^3 x^4 Exp[(-64/(9 Pi)) x^2]

In[5]:=

histogram = Histogram[#, {0.1}, PDF] & /@ gaps; plot = Plot[WignerSurmisePDF[x, #] , {x, 0, 3}] & /@ {1, 2, 4}; GraphicsRow@ MapThread[ Show[#1, #2, ImageSize -> 180, PlotLabel -> Row[{"\[Beta] = ", #3}]] &, {histogram, plot, {1, 2, 4}}]

Out[5]=