Wolfram 언어™

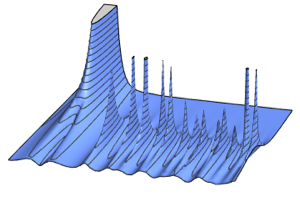
위샤트 분포와 역 위샤트 분포

위샤트 분포는 독립 다변량 정규 랜덤 벡터로부터 추출된 샘플의 공분산 행렬입니다. 이것은 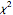분포를 다차원으로 일반화한 것입니다. 그러므로 이러한 분포는 자연적으로 회귀, 공분산 등 다변량 통계에서 사용되고 있습니다.

랜덤 정부호 행렬을 생성하고 위샤트 분포의 모수로 사용합니다.

In[1]:=

\[CapitalSigma] = DiagonalMatrix[RandomReal[10, 5]];

위샤트 분포의 행렬은 대칭 정부호 행렬입니다. »

In[2]:=

dist = WishartMatrixDistribution[30, \[CapitalSigma]]; mat = RandomVariate[dist];

In[3]:=

SymmetricMatrixQ[mat] && PositiveDefiniteMatrixQ[mat]

Out[3]=

역 위샤트 분포는 위샤트 분포의 역행렬 분포입니다. »

In[4]:=

invdist = InverseWishartMatrixDistribution[30, Inverse[\[CapitalSigma]]]; invmat = RandomVariate[invdist];

역 위샤트 분포의 행렬은 대칭 정부호 행렬입니다.

In[5]:=

SymmetricMatrixQ[invmat] && PositiveDefiniteMatrixQ[invmat]

Out[5]=

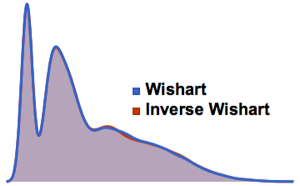
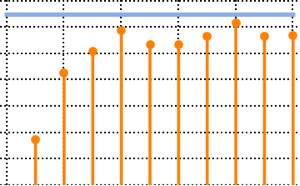
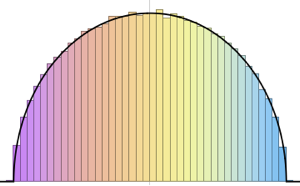
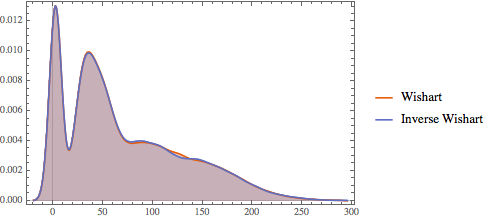
위샤트 분포와 역 위샤트 분포 행렬의 고유값의 분포를 비교합니다.

In[6]:=

eigs = Flatten[ RandomVariate[ MatrixPropertyDistribution[Eigenvalues[x], x \[Distributed] dist], 10^4]]; inveigs = Flatten[RandomVariate[ MatrixPropertyDistribution[Eigenvalues[x]^-1, x \[Distributed] invdist], 10^4]];

In[7]:=

SmoothHistogram[{eigs, inveigs}, PlotLegends -> {"Wishart", "Inverse Wishart"}, Filling -> Axis, ImageSize -> Medium, PlotTheme -> "Scientific"]

Out[7]=

임의의 비 제로 벡터 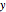와 스케일 행렬이 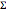인 위샤트 행렬 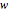에 대한 통계 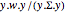는 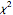분포입니다.

In[8]:=

y = #/Sqrt[#.\[CapitalSigma].#] &[RandomReal[1, 5]]; data = RandomVariate[ MatrixPropertyDistribution[y.w.y, w \[Distributed] WishartMatrixDistribution[30, \[CapitalSigma]]], 10^4];

In[9]:=

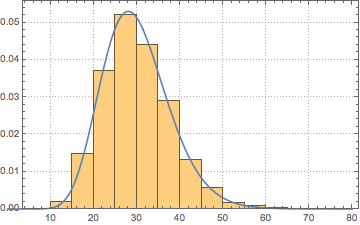
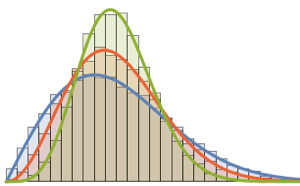
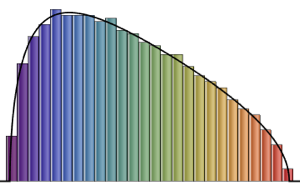
Show[Histogram[data, Automatic, PDF, PlotTheme -> "Detailed"], Plot[PDF[ChiSquareDistribution[30], x], {x, 0, 80}], ImageSize -> Medium]

Out[9]=