Wolfram 언어™

Tracy–Widom 분포

Tracy–Widom 분포는 가우시안 앙상블에 속하는 랜덤 행렬의 스케일된 최대 고유값의 극한 분포입니다. 이 분포는 계산 문제, 랜덤 성장 모델, 페이즈 전이 등의 다양한 분야에 사용되고 있으며, 정확한 예측을 제공합니다.

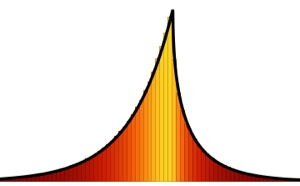
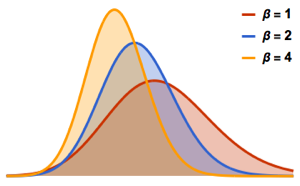
Tracy–Widom 분포는 각각 다른 가우시안 앙상블에 상응하는 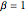, , 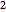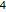세개의 클래스로 구성됩니다. 대응되는 확률 밀도 분포를 참조합니다.

In[1]:=

Plot[Table[ PDF[TracyWidomDistribution[\[Beta]], x], {\[Beta], {1, 2, 4}}] // Evaluate, {x, -5, 2}, Filling -> Axis, PlotLegends -> {"\[Beta] = 1", "\[Beta] = 2", "\[Beta] = 4"}, ImageSize -> Medium, PlotTheme -> "Detailed"]

Out[1]=

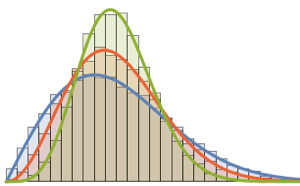
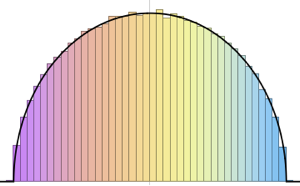
MatrixPropertyDistribution을 사용하여 가우시안 유니타리 앙상블에서 행렬의 스케일된 최대 고유값을 나타냅니다.

In[2]:=

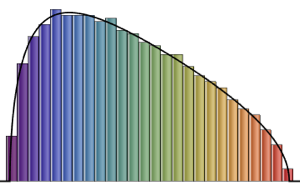
ev\[ScriptCapitalD][2, n_] := MatrixPropertyDistribution[(Max[Eigenvalues[x]] - 2 Sqrt[n]) n^(1/6), x \[Distributed] GaussianUnitaryMatrixDistribution[n]]

분포에서 샘플을 가지고 히스토그램을 확률 밀도 함수와 비교합니다.

In[3]:=

sample = RandomVariate[ev\[ScriptCapitalD][2, 250], 2000];

In[4]:=

Show[Histogram[sample, {0.2}, PDF, PlotTheme -> "Detailed"], Plot[PDF[TracyWidomDistribution[2], x ], {x, -5, 2}, PlotStyle -> Thick, PlotTheme -> "Detailed", PlotLegends -> None], ImageSize -> Medium]

Out[4]=

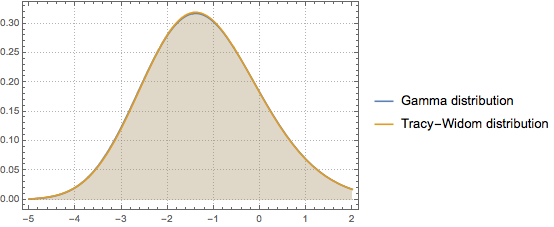
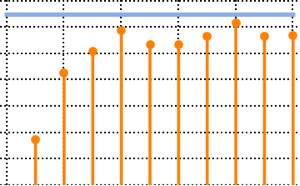
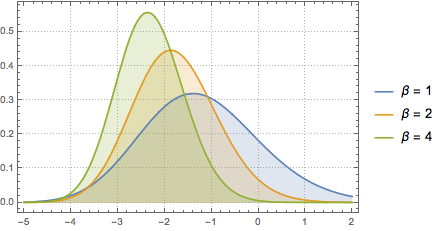
Tracy–Widom 분포의 중심 부분은 감마 분포에서 잘 근사 할 수있습니다.

In[5]:=

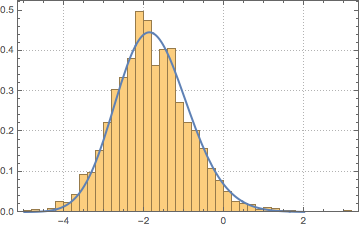
gdist = GammaDistribution[k, s, 1, a]; PDF[gdist, x]

Out[5]=

첫 세 모멘트를 매치시킴으로써 감마 분포를 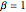Tracy–Widom 분포에 맞춥니다.

In[6]:=

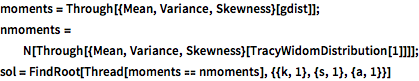
moments = Through[{Mean, Variance, Skewness}[gdist]]; nmoments = N[Through[{Mean, Variance, Skewness}[TracyWidomDistribution[1]]]]; sol = FindRoot[Thread[moments == nmoments], {{k, 1}, {s, 1}, {a, 1}}]

Out[6]=

확률 밀도 함수를 비교합니다.

In[7]:=

Plot[{PDF[gdist /. sol, x], PDF[TracyWidomDistribution[1], x]} // Evaluate, {x, -5, 2}, PlotLegends -> {"Gamma distribution", "Tracy-Widom distribution"}, Filling -> Axis, PlotTheme -> "Detailed", ImageSize -> Medium]

Out[7]=