Distribución de Tracy–Widom
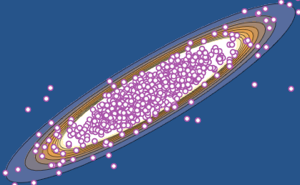
La distribcuión de Tracy–Widom es una distribución límite del valor propio escalado más grande de una matriz aleatoria perteneciente a conjuntos de Gauss. También aparece en varias disciplinas, tales como problemas de conteo, modelos de crecimiento aleatorios, transiciones de fase, etc., y proporciona predicciones precisas.
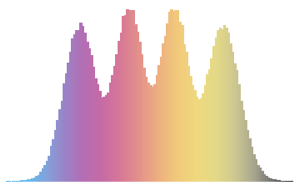
La distribución de Tracy–Widom consiste en tres clases  ,
,  y
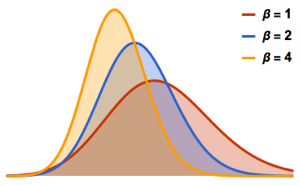
y  . Cada una corresponde a un conjunto de Gauss distinto; vea la correspondiente función de densidad de probabilidad.
. Cada una corresponde a un conjunto de Gauss distinto; vea la correspondiente función de densidad de probabilidad.

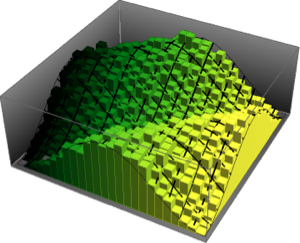
Use MatrixPropertyDistribution para representar el valor propio escalado más grande de una matriz de GUE.

ev\[ScriptCapitalD][2, n_] :=
MatrixPropertyDistribution[(Max[Eigenvalues[x]] - 2 Sqrt[n]) n^(1/6),
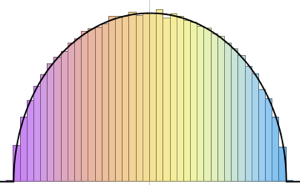
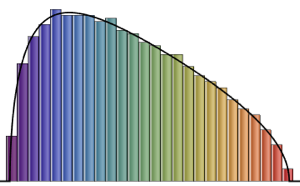
x \[Distributed] GaussianUnitaryMatrixDistribution[n]]Tome una muestra de la distribución y compare el histograma con la función de densidad de probabilidad.
sample = RandomVariate[ev\[ScriptCapitalD][2, 250], 2000];
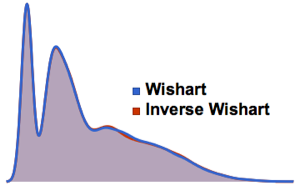
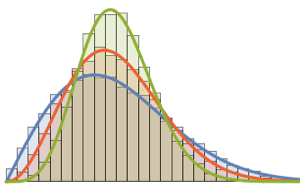
La distribución de Tracy–Widom puede ser bien aproximada por la distribución gamma en la región central.
gdist = GammaDistribution[k, s, 1, a];
PDF[gdist, x]
Ajuste la distribución gamma con la distribución de Tracy–Widom de  concordando los primeros tres momentos.
concordando los primeros tres momentos.

moments = Through[{Mean, Variance, Skewness}[gdist]];
nmoments =
N[Through[{Mean, Variance, Skewness}[TracyWidomDistribution[1]]]];
sol = FindRoot[Thread[moments == nmoments], {{k, 1}, {s, 1}, {a, 1}}]Compare las funciones de densidad de probabilidad.