Loi de Tracy–Widom
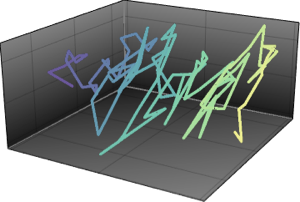
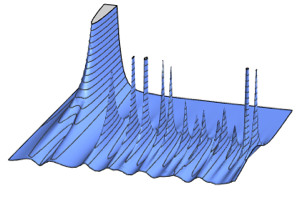
La loi de Tracy–Widom est la distribution limite de la plus grande valeur propre échelonnée d'une matrice aléatoire appartenant à des ensembles gaussiens. Elle apparaît également dans différentes disciplines, telles que les problèmes de comptage, les modèles de croissance aléatoire, les transitions de phase, etc. et donne des prédictions précises.
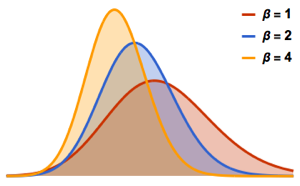
La loi de Tracy–Widom est composée de trois classes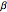 
, 
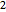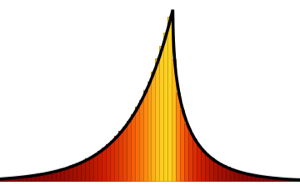
et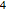 
. Chacune correspond à différents ensembles gaussiens. Découvrez la fonction correspondante de densité de probabilité.
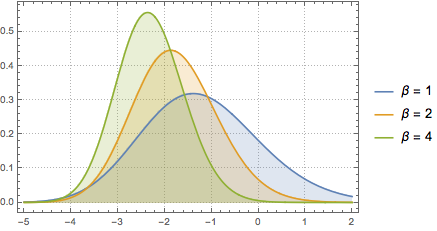
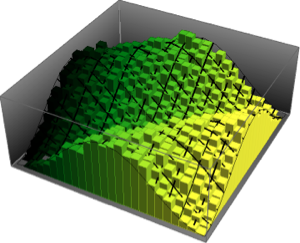
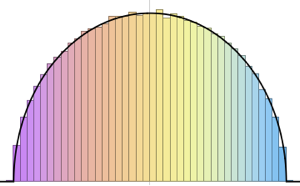
Utilisez MatrixPropertyDistribution pour représenter la plus grande valeur propre mise à l'échelle d'une matrice à partir de GUE.
ev\[ScriptCapitalD][2, n_] :=
MatrixPropertyDistribution[(Max[Eigenvalues[x]] - 2 Sqrt[n]) n^(1/6),
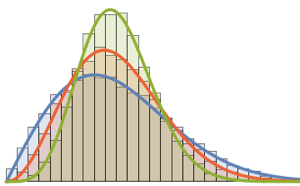
x \[Distributed] GaussianUnitaryMatrixDistribution[n]]Échantillonnez la distribution et comparez l'histogramme avec la fonction de densité de probabilité.
sample = RandomVariate[ev\[ScriptCapitalD][2, 250], 2000];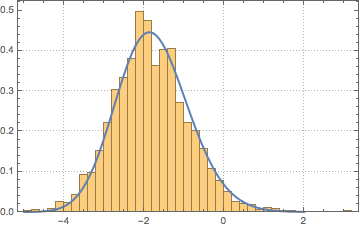
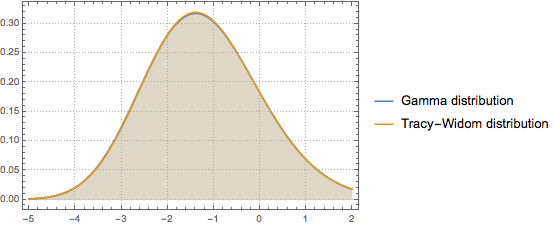
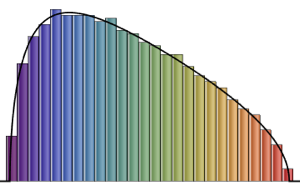
La loi de Tracy–Widom peut être bien approximée par une loi gamma dans la région centrale.
gdist = GammaDistribution[k, s, 1, a];
PDF[gdist, x]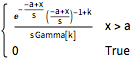
Ajustez la loi gamma avec la loi de Tracy–Widom de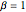 
en faisant correspondre les trois premiers moments.
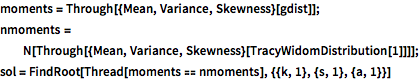
moments = Through[{Mean, Variance, Skewness}[gdist]];
nmoments =
N[Through[{Mean, Variance, Skewness}[TracyWidomDistribution[1]]]];
sol = FindRoot[Thread[moments == nmoments], {{k, 1}, {s, 1}, {a, 1}}]
Comparez les fonctions de densité de probabilité.
