Distribuição de Tracy–Widom

A distribuição de Tracy-Widom é uma distribuição limite do maior valor próprio escalado de uma matriz aleatória pertencente a conjuntos de Gauss. Também aparece em várias disciplinas diferentes, tais como problemas de contagem, modelos de crescimento aleatórios, transições de fase, etc., e dá previsões precisas.

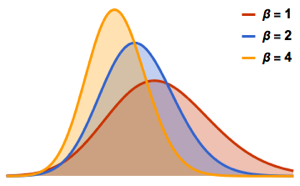
A distribuição de Tracy–Widom consiste em três classes 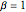, , 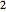and . Cada uma corresponde a um conjunto de Gauss diferente; veja a função densidade de probabilidade correspondente.

In[1]:=

Plot[Table[ PDF[TracyWidomDistribution[\[Beta]], x], {\[Beta], {1, 2, 4}}] // Evaluate, {x, -5, 2}, Filling -> Axis, PlotLegends -> {"\[Beta] = 1", "\[Beta] = 2", "\[Beta] = 4"}, ImageSize -> Medium, PlotTheme -> "Detailed"]

Out[1]=

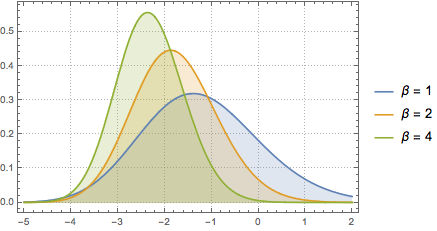
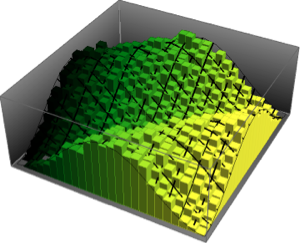
Use MatrixPropertyDistribution para representar o maior valor próprio escalado de uma matriz de GUE.

In[2]:=

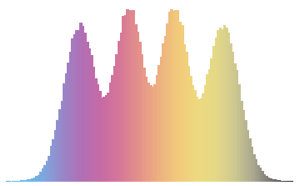
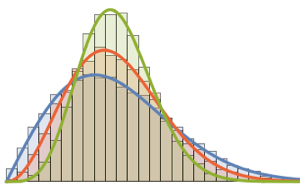
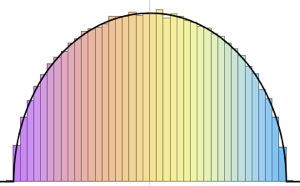
ev\[ScriptCapitalD][2, n_] := MatrixPropertyDistribution[(Max[Eigenvalues[x]] - 2 Sqrt[n]) n^(1/6), x \[Distributed] GaussianUnitaryMatrixDistribution[n]]

Faça uma amostra da distribuição e calcule o histograma com a função densidade de probabilidade.

In[3]:=

sample = RandomVariate[ev\[ScriptCapitalD][2, 250], 2000];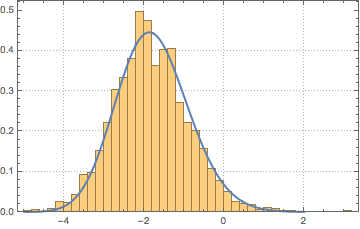

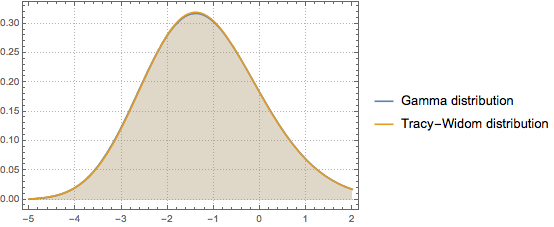
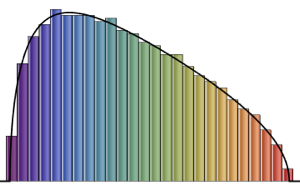
In[4]:=

Show[Histogram[sample, {0.2}, PDF, PlotTheme -> "Detailed"], Plot[PDF[TracyWidomDistribution[2], x ], {x, -5, 2}, PlotStyle -> Thick, PlotTheme -> "Detailed", PlotLegends -> None], ImageSize -> Medium]

Out[4]=

A distribuição Tracy–Widom pode ser bem aproximada pela distribuição gamma na região central.

In[5]:=

gdist = GammaDistribution[k, s, 1, a]; PDF[gdist, x]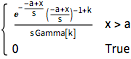

Out[5]=

Ajuste a distribuição gamma com a distribuição Tracy–Widom de 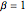concordando com os primeiros três momentos.

In[6]:=

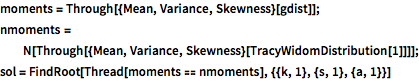
moments = Through[{Mean, Variance, Skewness}[gdist]]; nmoments = N[Through[{Mean, Variance, Skewness}[TracyWidomDistribution[1]]]]; sol = FindRoot[Thread[moments == nmoments], {{k, 1}, {s, 1}, {a, 1}}]

Out[6]=

Compare as funções densidade de probabilidade.

In[7]:=

Plot[{PDF[gdist /. sol, x], PDF[TracyWidomDistribution[1], x]} // Evaluate, {x, -5, 2}, PlotLegends -> {"Gamma distribution", "Tracy-Widom distribution"}, Filling -> Axis, PlotTheme -> "Detailed", ImageSize -> Medium]

Out[7]=