Tracy–Widom-Verteilung
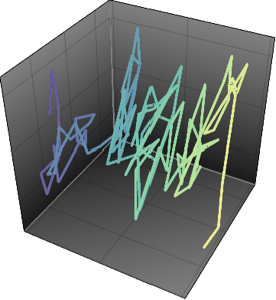
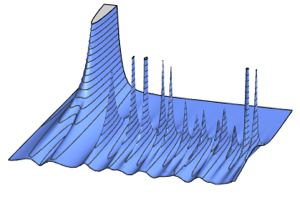
Die Tracy–Widom-Verteilung ist die Grenzverteilung der skalierten größten Eigenwerte einer Zufallsmatrix, die zu Gaußschen Ensembles gehört. Solche Verteilungen treten auch in zahlreichen anderen Disziplinen, wie bei Buchhaltungsproblemen, Modellen zufälligen Wachstums, Phasenübergängen etc. auf und liefern akkurate Prognosen.
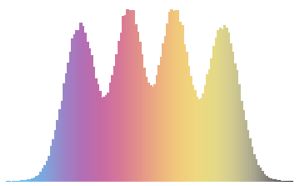
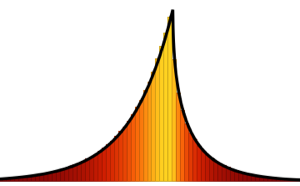
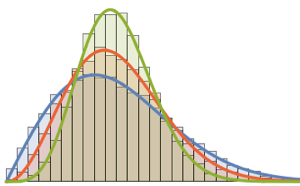
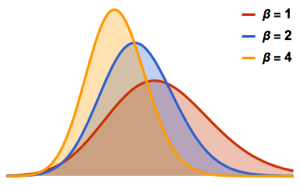
Die Tracy–Widom-Verteilung besteht aus drei Klassen 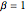 ,
, 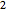 und
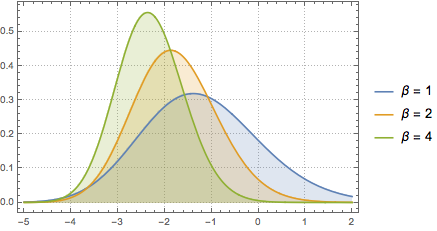
und  . Jede entspricht einem anderen Gaußschen Ensemble; beachten Sie auch die entsprechenden WDFs.
. Jede entspricht einem anderen Gaußschen Ensemble; beachten Sie auch die entsprechenden WDFs.
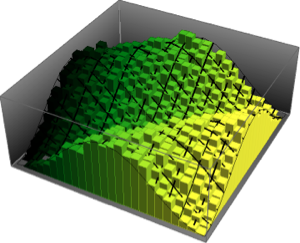
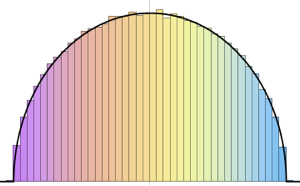
Verwenden Sie MatrixPropertyDistribution, um den skalierten größten Eigenwert einer Matrix eines GUE darzustellen.

ev\[ScriptCapitalD][2, n_] :=
MatrixPropertyDistribution[(Max[Eigenvalues[x]] - 2 Sqrt[n]) n^(1/6),
x \[Distributed] GaussianUnitaryMatrixDistribution[n]]Nehmen Sie eine Stichprobe aus der Verteilung und vergleichen Sie das Histogramm mit der WDF.
sample = RandomVariate[ev\[ScriptCapitalD][2, 250], 2000];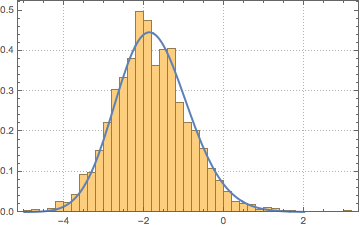
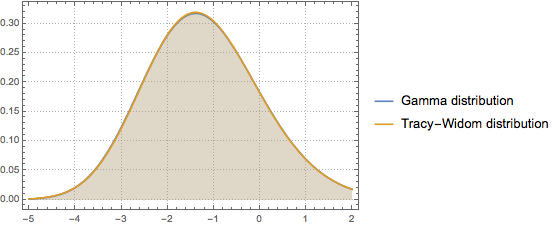
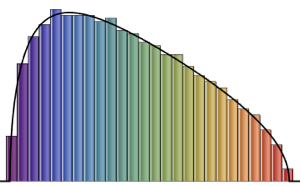
Die Tracy–Widom-Verteilung kann gut durch eine Gammaverteilung im mittleren Bereich approximiert werden.
gdist = GammaDistribution[k, s, 1, a];
PDF[gdist, x]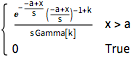
Führen Sie eine Kurvenanpassung der Gammaverteilung mit der Tracy–Widom-Verteilung von 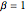 durch, so dass die ersten drei Momente übereinstimmen.
durch, so dass die ersten drei Momente übereinstimmen.
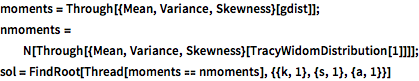
moments = Through[{Mean, Variance, Skewness}[gdist]];
nmoments =
N[Through[{Mean, Variance, Skewness}[TracyWidomDistribution[1]]]];
sol = FindRoot[Thread[moments == nmoments], {{k, 1}, {s, 1}, {a, 1}}]Vergleichen Sie die WDFs.