トレーシー・ウィダム分布

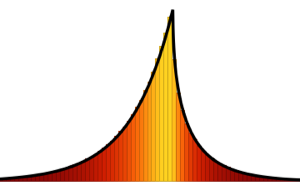
トレーシー・ウィダム分布は，ガウス型アンサンブルに属すランダム行列のスケールされた最大固有値の極限分布である．この分布は，計数問題，ランダム成長モデル，相転移等のさまざまな分野に使用されており，正確な予測を与える．

トレーシー・ウィダム分布は，それぞれが異なるガウス型アンサンブルに属す 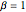, , 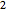の3つのクラスからなる．対応する確率密度分布を参照のこと．

In[1]:=

Plot[Table[ PDF[TracyWidomDistribution[\[Beta]], x], {\[Beta], {1, 2, 4}}] // Evaluate, {x, -5, 2}, Filling -> Axis, PlotLegends -> {"\[Beta] = 1", "\[Beta] = 2", "\[Beta] = 4"}, ImageSize -> Medium, PlotTheme -> "Detailed"]

Out[1]=

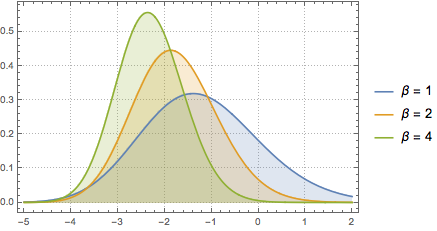
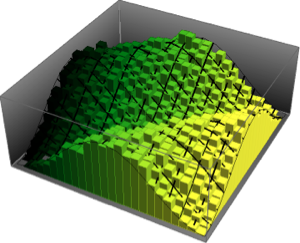
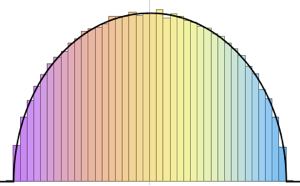
MatrixPropertyDistributionを使ってガウス型ユニタリアンサンブルからの行列のスケールされた最大固有値を表す．

In[2]:=

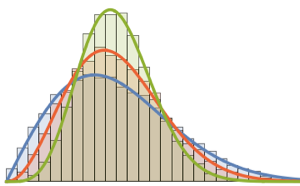
ev\[ScriptCapitalD][2, n_] := MatrixPropertyDistribution[(Max[Eigenvalues[x]] - 2 Sqrt[n]) n^(1/6), x \[Distributed] GaussianUnitaryMatrixDistribution[n]]

分布からサンプルを取り，そのヒストグラムを確率密度関数と比較する．

In[3]:=

sample = RandomVariate[ev\[ScriptCapitalD][2, 250], 2000];

In[4]:=

Show[Histogram[sample, {0.2}, PDF, PlotTheme -> "Detailed"], Plot[PDF[TracyWidomDistribution[2], x ], {x, -5, 2}, PlotStyle -> Thick, PlotTheme -> "Detailed", PlotLegends -> None], ImageSize -> Medium]

Out[4]=

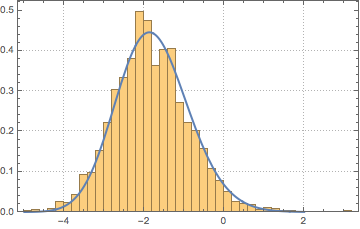
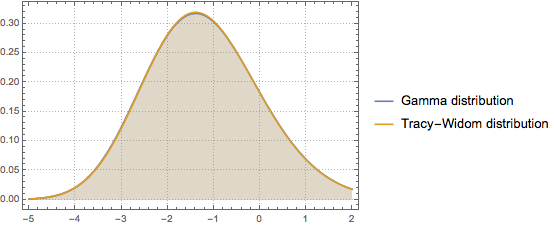
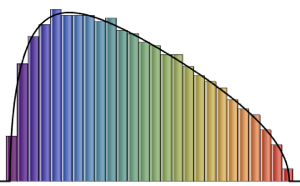
トレーシー・ウィダム分布の中心部分はガンマ分布でうまく近似することができる．

In[5]:=

gdist = GammaDistribution[k, s, 1, a]; PDF[gdist, x]

Out[5]=

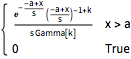
最初の3モーメントをマッチさせることで，ガンマ分布を 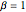のトレーシー・ウィダム分布にフィットする．

In[6]:=

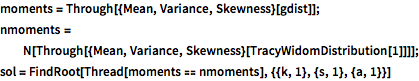
moments = Through[{Mean, Variance, Skewness}[gdist]]; nmoments = N[Through[{Mean, Variance, Skewness}[TracyWidomDistribution[1]]]]; sol = FindRoot[Thread[moments == nmoments], {{k, 1}, {s, 1}, {a, 1}}]

Out[6]=

確率密度関数を比較する．

In[7]:=

Plot[{PDF[gdist /. sol, x], PDF[TracyWidomDistribution[1], x]} // Evaluate, {x, -5, 2}, PlotLegends -> {"Gamma distribution", "Tracy-Widom distribution"}, Filling -> Axis, PlotTheme -> "Detailed", ImageSize -> Medium]

Out[7]=