Wolfram 语言™

特雷西–维多姆分布

特雷西–维多姆分布是属于高斯系综的随机矩阵的缩放最大特征值的极限分布. 它也出现在各种不同学科中，例如计数问题、随机增长模型、相变等，并给出准确的预测.

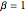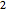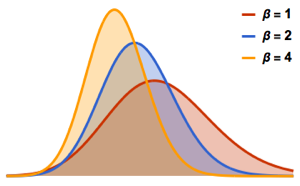
特雷西–维多姆分布由 、 和 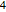三类组成. 每一类都对应于不同的高斯系综；详见相应的概率密度函数.

In[1]:=

Plot[Table[ PDF[TracyWidomDistribution[\[Beta]], x], {\[Beta], {1, 2, 4}}] // Evaluate, {x, -5, 2}, Filling -> Axis, PlotLegends -> {"\[Beta] = 1", "\[Beta] = 2", "\[Beta] = 4"}, ImageSize -> Medium, PlotTheme -> "Detailed"]

Out[1]=

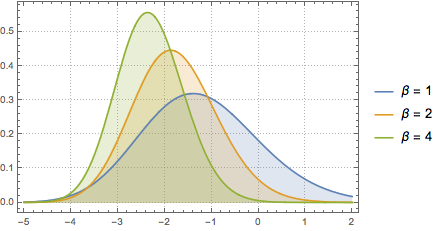
使用 MatrixPropertyDistribution 表示来自于 GUE 的矩阵的缩放最大特征值.

In[2]:=

ev\[ScriptCapitalD][2, n_] := MatrixPropertyDistribution[(Max[Eigenvalues[x]] - 2 Sqrt[n]) n^(1/6), x \[Distributed] GaussianUnitaryMatrixDistribution[n]]

从分布采样，并比较直方图与概率密度函数.

In[3]:=

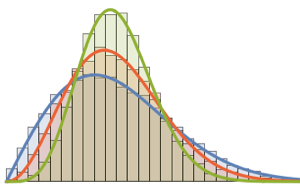
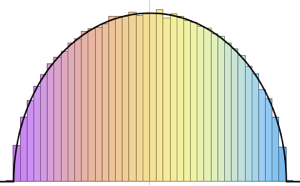
sample = RandomVariate[ev\[ScriptCapitalD][2, 250], 2000];

In[4]:=

Show[Histogram[sample, {0.2}, PDF, PlotTheme -> "Detailed"], Plot[PDF[TracyWidomDistribution[2], x ], {x, -5, 2}, PlotStyle -> Thick, PlotTheme -> "Detailed", PlotLegends -> None], ImageSize -> Medium]

Out[4]=

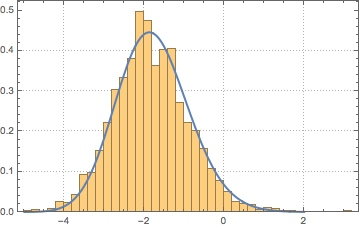
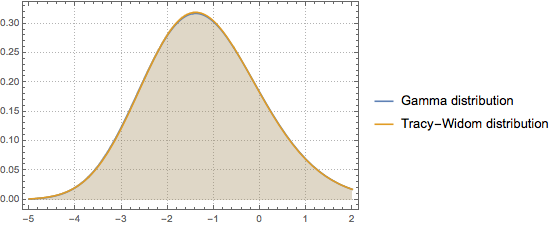
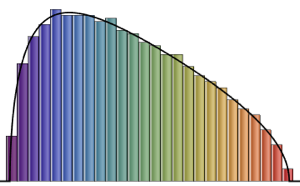
特雷西–维多姆分布可以通过中央区域的伽玛分布很好地逼近.

In[5]:=

gdist = GammaDistribution[k, s, 1, a]; PDF[gdist, x]

Out[5]=

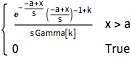
通过匹配前三个矩量，用 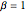的特雷西–维多姆分布拟合伽玛分布.

In[6]:=

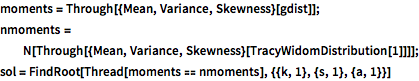
moments = Through[{Mean, Variance, Skewness}[gdist]]; nmoments = N[Through[{Mean, Variance, Skewness}[TracyWidomDistribution[1]]]]; sol = FindRoot[Thread[moments == nmoments], {{k, 1}, {s, 1}, {a, 1}}]

Out[6]=

比较概率密度函数.

In[7]:=

Plot[{PDF[gdist /. sol, x], PDF[TracyWidomDistribution[1], x]} // Evaluate, {x, -5, 2}, PlotLegends -> {"Gamma distribution", "Tracy-Widom distribution"}, Filling -> Axis, PlotTheme -> "Detailed", ImageSize -> Medium]

Out[7]=