EntityStore de transformadas integrales

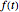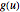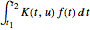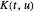Una transformada integral es una operación matemática que mapea una función con otra por medio de una integral de la forma donde se conoce como un núcleo. Las transformadas integrales son extremadamente importantes en muchas áreas, incluyendo el procesamiento de señales, imágenes médicas y teoría de la probabilidad. Aquí se ilustra la construcción de un almacén de entidades que contiene propiedades de importantes transformadas.

El almacén de entidades puede ser codificado a mano grabando las propiedades más importantes de las transformadas integrales en una estructura de datos de EntityStore.

In[1]:=

EntityStore[<| "Types" -> <| "IntegralTransform" -> <| "Entities" -> <| "ExponentialFourierTransform" -> <| "Label" -> "exponential Fourier transform", "StandardName" -> "ExponentialFourierTransform", "StandardNotation" -> Hold[f[t]], "Definition" -> Inactive[FourierTransform][f[t], t, z] \!\(\* TagBox["==", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"=="]\) Inactive[Integrate][ E^(I t z) f[t], {t, -\[Infinity], \[Infinity]}]/Sqrt[ 2 \[Pi]], "GeneralProperties" -> <| "Linearity" -> {Inactive[FourierTransform][ a f[t] + b g[t], t, z] \!\(\* TagBox["==", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"=="]\) a Inactive[FourierTransform][f[t], t, z] + b Inactive[FourierTransform][g[t], t, z], Inactive[FourierTransform][f[t], t, z] \!\(\* TagBox["==", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"=="]\) Inactive[FourierTransform][f[-t] UnitStep[t], t, -z] + Inactive[FourierTransform][f[t] UnitStep[t], t, z]}, "Reflection" -> {Inactive[FourierTransform][f[-t], t, z] \!\(\* TagBox["==", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"=="]\) Inactive[FourierTransform][f[t], t, -z]}, "Dilation" -> {ConditionalExpression[ Inactive[FourierTransform][f[a t], t, z] \!\(\* TagBox["==", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"=="]\) Inactive[FourierTransform][f[t], t, z/a]/Abs[a], a \!\(\* TagBox["\[Element]", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"\[Element]"]\) Reals && a \!\(\* TagBox["!=", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"!="]\) 0]}, "Shifting or translation" -> {ConditionalExpression[ Inactive[FourierTransform][f[-a + t], t, z] \!\(\* TagBox["==", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"=="]\) E^(I a z) Inactive[FourierTransform][f[t], t, z], a \!\(\* TagBox["\[Element]", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"\[Element]"]\) Reals]}|>|>|>|>|>|>]

Out[1]=

Una versión más completa puede ser encontrada en el siguiente CloudObject.

In[2]:=

itstore = CloudGet[CloudObject[ "https://www.wolframcloud.com/objects/c21b356b-607a-406c-af91-\ 5088f435fe99"]]

Out[2]=

Registre el almacén para esta sesión.

In[3]:=

PrependTo[$EntityStores, itstore];

Vea las entidades en el almacén.

In[4]:=

EntityValue["IntegralTransform", "Entities"]

Out[4]=

Agregue una nueva transformada.

In[5]:=

Entity["IntegralTransform", "HilbertTransform"]["Label"] = "Hilbert transform"; Entity["IntegralTransform", "HilbertTransform"]["Definition"] = Inactive[HilbertTransform][f[t], t, x] \!\(\* TagBox["==", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"=="]\) 1/\[Pi] Inactive[Integrate][f[t]/( t - x), {t, -\[Infinity], \[Infinity]}, PrincipalValue -> True, Assumptions -> x \!\(\* TagBox["\[Element]", "InactiveToken", BaseStyle->"Inactive", SyntaxForm->"\[Element]"]\) Reals];

Recupere las propiedades actuales disponibles para transformadas integrales.

In[6]:=

EntityValue["IntegralTransform", "Properties"]

Out[6]=

Recupere las definiciones para transformadas exponenciales de Fourier y Mellin.

In[7]:=

EntityValue[ Entity["IntegralTransform", "LaplaceTransform"], "Definition"]

Out[7]=

In[8]:=

EntityValue[ Entity["IntegralTransform", "MellinTransform"], "Definition"]

Out[8]=

Compare con las expresiones dadas por las correspondientes funciones incorporadas.

In[9]:=

Activate[EntityValue[Entity["IntegralTransform", "LaplaceTransform"], "Definition"][[2]] /. f :> Function[t, ArcTan[t]]]

Out[9]=

In[10]:=

LaplaceTransform[ArcTan[t], t, z]

Out[10]=

Muestre la propiedad de convolución de la transformada Z.

In[11]:=

Entity["IntegralTransform", "ZTransform"][ "GeneralProperties"]["Convolution"]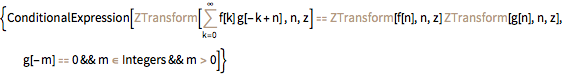

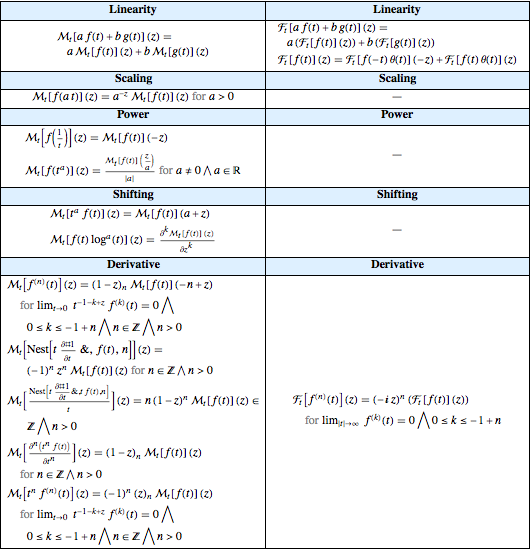
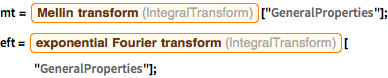
Out[11]=

Compare las propiedades actualmente almacenadas de las transformadas exponenciales de Fourier y Mellin.

In[12]:=

format[l_] := If[MatchQ[l, _Missing], "\[LongDash]", Activate[HoldForm @@ ({Column[l]} /. HoldPattern[ConditionalExpression[a_, b_]] :> Row[{a, Style[ " for ", Gray], b}])]]

In[13]:=

mt = Entity["IntegralTransform", "MellinTransform"][ "GeneralProperties"]; eft = Entity["IntegralTransform", "ExponentialFourierTransform"][ "GeneralProperties"];

In[14]:=

Grid[Take[ Flatten[{{Style[#, Bold], Style[#, Bold]}, {format@mt[#], format@eft[#]}} & /@ DeleteDuplicates[Join[Keys[mt], Keys[eft]]], 1], 10], Dividers -> All, Background -> {None, {{LightBlue, White}}}] // TraditionalForm

Out[14]//TraditionalForm=