Wolfram Language™

Evalúe una bolsa de monedas

Una bolsa de monedas estadounidenses nuevas es robada de un banco. Sin abrir la bolsa, ¿qué se puede decir del valor monetario de sus contenidos? Una característica física obvia que se puede medir fácilmente es el peso de la bolsa. Suponiendo que es una bolsa de monedas de una libra, combine los conocimientos técnicos de Wolfram Knowledgebase sobre monedas con la habilidad incorporada para solucionar ecuaciones lineares, para estudiar el valor esperado del botín.

Para empezar, genere una lista de monedas estadounidenses en circulación actual por medio de una clase de entidades implícitamente definida.

In[1]:=

EntityClass["CurrencyDenomination", {EntityProperty[ "CurrencyDenomination", "IssuingCountry"] -> Entity["Country", "UnitedStates"], EntityProperty["CurrencyDenomination", "Format"] -> "coin"}]

Out[1]=

Expanda la clase de entidades implícitamente definida haciendo clic en [+], encuentre sus miembros, y ordénelos por valor.

In[2]:=

coinsUS = EntityList[ EntityClass[ "CurrencyDenomination", { EntityProperty[ "CurrencyDenomination", "IssuingCountry"] -> Entity[ "Country", "UnitedStates"], EntityProperty["CurrencyDenomination", "Format"] -> "coin"}]] // SortBy[#[EntityProperty["CurrencyDenomination", "Value"]] &]

Out[2]=

Cree un collage de imágenes de moneda.

In[3]:=

ImageCollage[ EntityValue[coinsUS, EntityProperty["CurrencyDenomination", "Image"]], Background -> White]

Out[3]=

Resuma las propiedades de las monedas en una tabla.

In[4]:=

TextGrid[{ImageResize[#2, 60], #1, Row[Riffle[#3, Style[" | ", Gray]]]} & @@@ EntityValue[ coinsUS, {EntityProperty["CurrencyDenomination", "Entity"], EntityProperty["CurrencyDenomination", "Image"], EntityProperty["CurrencyDenomination", "PeopleOnCurrency"]}], Alignment -> {Left, Center}, Dividers -> All] // TraditionalForm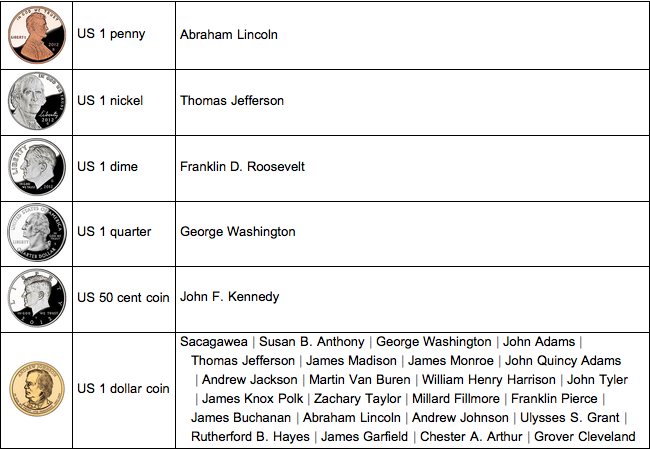

Out[4]//TraditionalForm=

Obtenga denominaciones (en centavos) y masas (en gramos) de monedas y convierta las masas en números racionales.

In[5]:=

{values, masses} = Transpose[EntityValue[coinsUS, {"Value", "Weight"}]]

Out[5]=

In[6]:=

coinsandweights = Transpose[{ QuantityMagnitude[UnitConvert[values, "USCents"]], Rationalize[QuantityMagnitude[N[UnitConvert[masses, "Grams"]]]] }]

Out[6]=

In[7]:=

lcm = LCM @@ Denominator[Rationalize[coinsandweights][[All, 2]]];

In[8]:=

rationalcoinweights = lcm #2 & @@@ Rationalize[coinsandweights]

Out[8]=

Encuentre todas las distribuciones de monedas que son compatibles con una medida de peso de una libra con un error de medición de ± 0.1% (asumiendo que la bolsa misma contribuye de forma no significativa).

In[9]:=

meanWeight = QuantityMagnitude[UnitConvert[Quantity[1, "Pounds"], "Grams"]];

In[10]:=

error = Normal[Quantity[0.1, "Percent"]];

In[11]:=

{minScaledWeight, maxScaledWeight} = {Floor[lcm meanWeight (1 - error/2)], Ceiling[lcm meanWeight (1 + error/2)]}

Out[11]=

Use FrobeniusSolve para determinar todas las posibles colecciones de moneda dando el peso total requerido.

In[12]:=

allSolutions = Monitor[ Table[fb = FrobeniusSolve[rationalcoinweights, scaledweight], {scaledweight, minScaledWeight, maxScaledWeight}], Row[{NumberForm[ 100. (scaledweight - minScaledWeight)/(maxScaledWeight - minScaledWeight), {4, 1}, "NumberPadding" -> {" ", "0"}], "%: ", Length[fb], " solutions"}] ];

In[13]:=

Flatten[allSolutions, 1] // Length

Out[13]=

Encuentre el mínimo, la mediana, la media y el máximo de los valores monetarios totales de las monedas en la bolsa (asumiendo que todas las combinaciones son igualmente probables).

In[14]:=

coins = coinsandweights[[All, 1]];

In[15]:=

dollarValues = (coins.#/100.) & /@ Flatten[allSolutions, 1];

In[16]:=

TextGrid[With[{stats = {Min, Median, Mean, Max}}, Transpose[{stats, NumberForm[Quantity[#, "USDollars"], {\[Infinity], 2}] & /@ Through[stats[dollarValues]]}]], Alignment -> {{Left, Decimal}}, Dividers -> All, Background -> {Automatic, {{LightBlue, None}}}] // TraditionalForm

Out[16]//TraditionalForm=

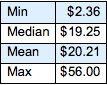
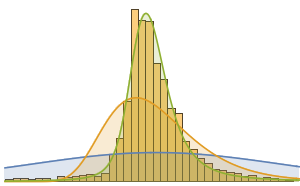
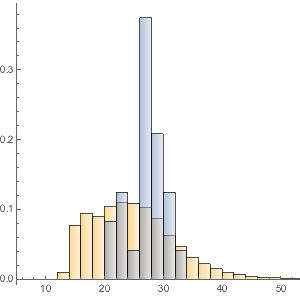
Cree un histograma de la distribución del valor monetario total.

In[17]:=

Histogram[dollarValues, Automatic, "PDF", AxesLabel -> {Quantity[None, "USDollars"], "fraction"}]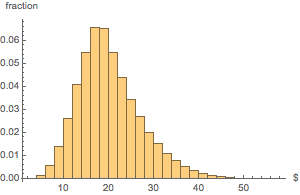

Out[17]=

La distribución de peso de todas las bolsas es bastante uniforme.

In[18]:=

weights = coinsandweights[[All, -1]]; lbg = QuantityMagnitude[UnitConvert[Quantity[1, "Pounds"], "Grams"]]; weightvalues = (weights.#)/lbg & /@ Flatten[allSolutions, 1];

In[19]:=

Histogram[weightvalues, 50, "PDF", AxesLabel -> {Quantity[None, "USDollars"], "fraction"}]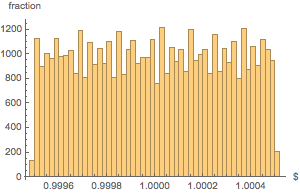

Out[19]=

Represente gráficamente la distribución del número de monedas.

In[20]:=

Histogram[Total /@ Flatten[allSolutions, 1], {5}]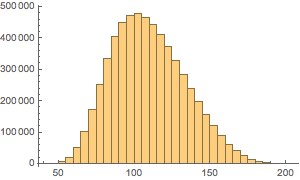

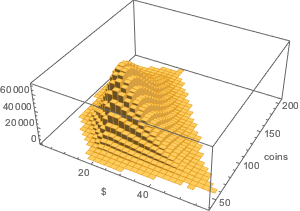
Out[20]=

La distribución bivariante del valor monetario versus el número de monedas en la bolsa.

In[21]:=

Histogram3D[{coins.#/100., Total[#]} & /@ Flatten[allSolutions, 1], AxesLabel -> {Quantity[None, "USDollars"], "coins"}]

Out[21]=