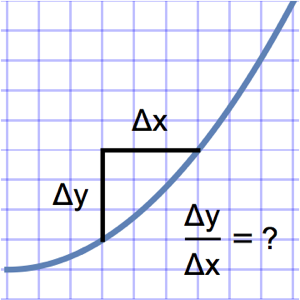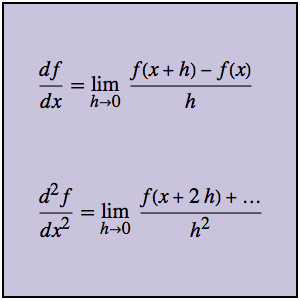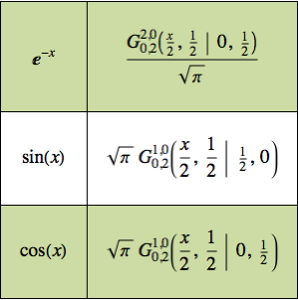Modellieren Sie eine hängende Kette
Ermitteln Sie die Stelle minimaler potentieller Energie einer Kette oder eines Kabels der Länge 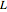 , das zwischen zwei Punkten aufgehängt ist.
, das zwischen zwei Punkten aufgehängt ist.
Legen Sie Parameterwerte für die Länge der Kette 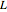 , die Höhe am linken Ende
, die Höhe am linken Ende 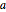 sowie die Höhe am rechten Ende
sowie die Höhe am rechten Ende 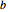 fest.
fest.
L = 4; a = 1; b = 3; 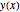 sei die Höhe der Kette als eine Funktion der horizontalen Position, mit
sei die Höhe der Kette als eine Funktion der horizontalen Position, mit 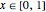 .
.
xf = 1; nh = 201; h := xf/nh;Legen Sie Variablen für die Höhe der Kette 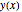 fest.
fest.
varsy = Array[y, nh + 1, {0, nh}];Geben Sie die Neigung an der Stelle 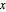 mit
mit 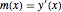 an und legen Sie dafür Variablen fest.
an und legen Sie dafür Variablen fest.
varsm = Array[m, nh + 1, {0, nh}];Geben Sie die partielle potentielle Energie von 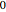 bis
bis 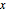 mit
mit 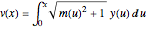 an.
an.
varsv = Array[v, nh + 1, {0, nh}];Geben Sie die Länge der Kette an der Stelle 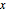 mit
mit 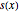 an und legen Sie Variablen dafür fest.
an und legen Sie Variablen dafür fest.
varss = Array[s, nh + 1, {0, nh}];Verknüpfen Sie alle Variablen.
vars = Join[varsm, varsy, varsv, varss];Das Ziel ist, die potentielle Gesamtenergie 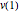 zu minimieren.
zu minimieren.
objfn = v[nh];Hier sind die der Geometrie zugrundeliegenden Randwertsbedingungen.
bndcons = {y[0] == a, y[nh] == b, v[0] == 0, s[0] == 0, s[nh] == L}; Diskretisieren Sie die ODE: 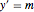 ,
, 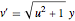 ,
, 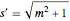 .
.
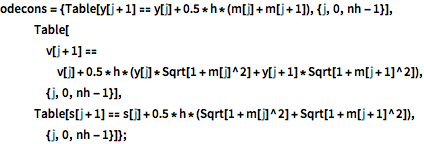
odecons = {Table[
y[j + 1] == y[j] + 0.5*h*(m[j] + m[j + 1]), {j, 0, nh - 1}],
Table[v[j + 1] ==
v[j] + 0.5*
h*(y[j]*Sqrt[1 + m[j]^2] + y[j + 1]*Sqrt[1 + m[j + 1]^2]), {j,
0, nh - 1}],
Table[s[j + 1] ==
s[j] + 0.5*h*(Sqrt[1 + m[j]^2] + Sqrt[1 + m[j + 1]^2]), {j, 0,
nh - 1}]};Wählen Sie Anfangspunkte für die Variablen.

tmin = If[b > a, 0.25 , 0.75]; init =
Join[Table[4*Abs[b - a]*((k/nh) - tmin), {k, 0, nh}],
Table[4*Abs[b - a]*(k/nh)*(0.5*(k/nh) - tmin) + a, {k, 0, nh}],
Table[(4*Abs[b - a]*(k/nh)*(0.5*(k/nh) - tmin) + a)*4*
Abs[b - a]*((k/nh) - tmin), {k, 0, nh}],
Table[4*Abs[b - a]*((k/nh) - tmin), {k, 0, nh}]];Minimieren Sie die den Bedingungen unterliegende potentielle Gesamtenergie.
sol = FindMinimum[{objfn, Join[bndcons, odecons]},
Thread[{vars, init}]];Extrahieren Sie die Lösungspunkte.
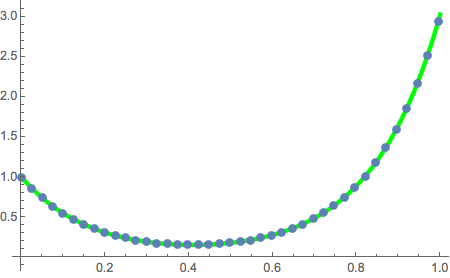
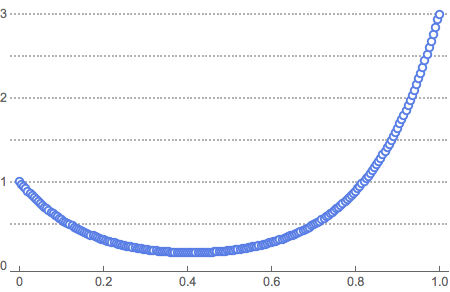
solpts = Table[{i h, y[i] /. sol[[2]]}, {i, 0, nh}];Plotten Sie die Stelle der Kette mit minimaler potentieller Energie.
ListPlot[solpts, ImageSize -> Medium, PlotTheme -> "Marketing"]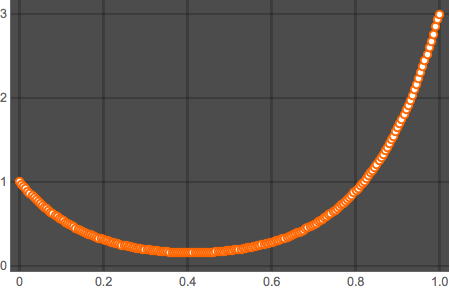
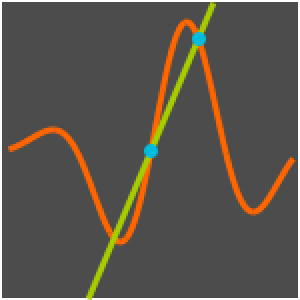
Ermitteln Sie mit FindFit das beste Modell zur Anpassung an die Kettenkurve.
catenary[t_] = c1 + (1/c2) Cosh[c2 (t - c3)];fitsol = FindFit[solpts, catenary[t], {c1, c2, c3}, {t}]Plotten Sie die Lösungspunkte zusammen mit der Kettenlinie.

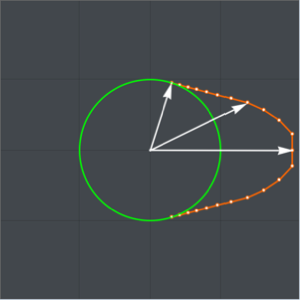
Show[Plot[catenary[t] /. fitsol, {t, 0, 1},
PlotStyle -> Directive[Green, Thickness[0.01]],
ImageSize -> Medium],
ListPlot[Take[solpts, 1 ;; nh ;; 5], PlotStyle -> PointSize[.02]]]