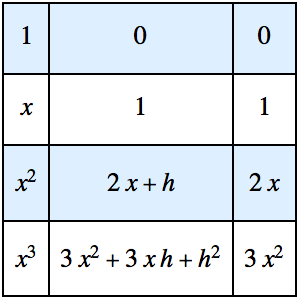
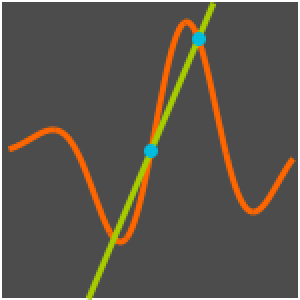
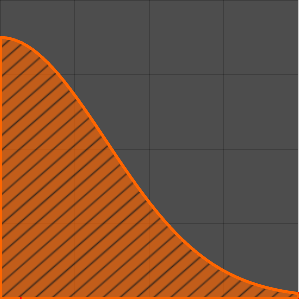
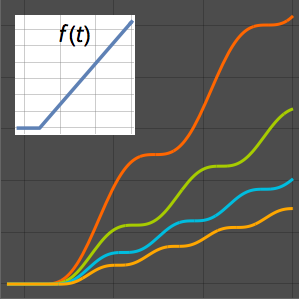
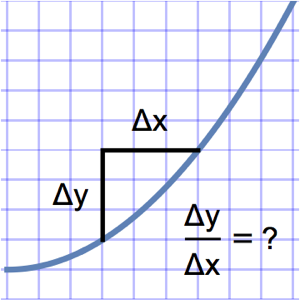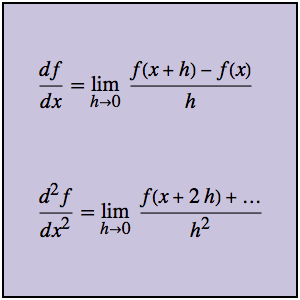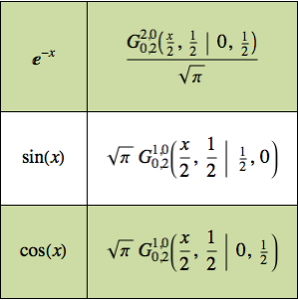Создание модели подвесной цепи
Найти положение с минимальной потенциальной энергией цепи или кабеля длины 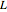 , провесающей между двумя точками.
, провесающей между двумя точками.
Задать значения параметров для длины цепи 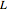 , высоты левого конца
, высоты левого конца 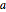 , и высоты правого конца
, и высоты правого конца 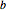 .
.
L = 4; a = 1; b = 3; Допустим, что 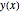 является высотой цепи в функции горизонтальной позиции с
является высотой цепи в функции горизонтальной позиции с 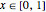 .
.
xf = 1; nh = 201; h := xf/nh;Задать переменные для высоты цепи 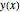 .
.
varsy = Array[y, nh + 1, {0, nh}];Указать уклон в положении 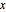 через
через 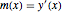 и задать его величину.
и задать его величину.
varsm = Array[m, nh + 1, {0, nh}];Указать частичную потенциальную энергию от 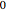 до
до 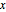 через
через 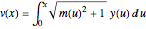 .
.
varsv = Array[v, nh + 1, {0, nh}];Указать длину цепи в положении 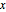 через
через 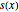 и задать её величинy.
и задать её величинy.
varss = Array[s, nh + 1, {0, nh}];Объединить все величины.
vars = Join[varsm, varsy, varsv, varss];Цель данного шага - минимизировать общую потенциальную энергию 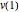 .
.
objfn = v[nh];Ниже представлены ограничения предельных значений, основанные на геометрическом строении.
bndcons = {y[0] == a, y[nh] == b, v[0] == 0, s[0] == 0, s[nh] == L};Дискретизировать обыкновенные дифференциальные уравнения: 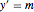 ,
, 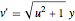 ,
, 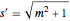 .
.
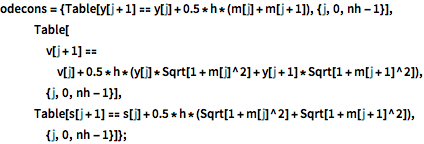
odecons = {Table[
y[j + 1] == y[j] + 0.5*h*(m[j] + m[j + 1]), {j, 0, nh - 1}],
Table[v[j + 1] ==
v[j] + 0.5*
h*(y[j]*Sqrt[1 + m[j]^2] + y[j + 1]*Sqrt[1 + m[j + 1]^2]), {j,
0, nh - 1}],
Table[s[j + 1] ==
s[j] + 0.5*h*(Sqrt[1 + m[j]^2] + Sqrt[1 + m[j + 1]^2]), {j, 0,
nh - 1}]};Выберать начальные точки для величин.

tmin = If[b > a, 0.25 , 0.75]; init =
Join[Table[4*Abs[b - a]*((k/nh) - tmin), {k, 0, nh}],
Table[4*Abs[b - a]*(k/nh)*(0.5*(k/nh) - tmin) + a, {k, 0, nh}],
Table[(4*Abs[b - a]*(k/nh)*(0.5*(k/nh) - tmin) + a)*4*
Abs[b - a]*((k/nh) - tmin), {k, 0, nh}],
Table[4*Abs[b - a]*((k/nh) - tmin), {k, 0, nh}]];Минимизировать общую потенциальную энергию, основываясь на ограничениях.
sol = FindMinimum[{objfn, Join[bndcons, odecons]},
Thread[{vars, init}]];Извлечь точки решения.
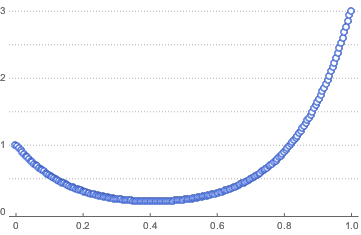
solpts = Table[{i h, y[i] /. sol[[2]]}, {i, 0, nh}];Графически изобразить положение цепи с минимальной потенциальной энергией.
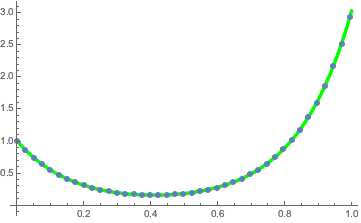
ListPlot[solpts, ImageSize -> Medium, PlotTheme -> "Marketing"]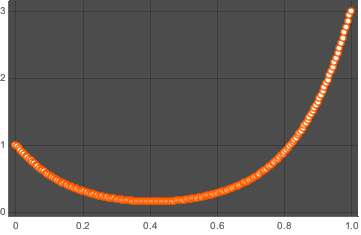
Используйте FindFit для подгонки результата до цепной линии.
catenary[t_] = c1 + (1/c2) Cosh[c2 (t - c3)];fitsol = FindFit[solpts, catenary[t], {c1, c2, c3}, {t}]Графически изобразите точки решения вместе с цепной линией.

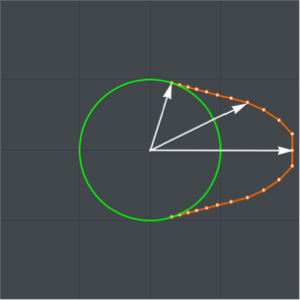
Show[Plot[catenary[t] /. fitsol, {t, 0, 1},
PlotStyle -> Directive[Green, Thickness[0.01]],
ImageSize -> Medium],
ListPlot[Take[solpts, 1 ;; nh ;; 5], PlotStyle -> PointSize[.02]]]