建立一个吊链模型: Wolfram语言 11 的新功能

‹›

建立一个吊链模型

找出悬挂在两点间长度为 L 的链条或缆绳在势能最小时的位置.

设置链条长度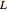、左端高度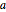和右端高度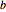的值.

In[1]:=

L = 4; a = 1; b = 3;

令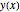为链条高度，它是水平位置的函数，其中 .

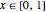In[2]:=

xf = 1; nh = 201; h := xf/nh;

为链条高度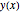设置变量.

In[3]:=

varsy = Array[y, nh + 1, {0, nh}];

用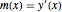表示在位置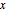处的斜率，并为之设置变量.

In[4]:=

varsm = Array[m, nh + 1, {0, nh}];

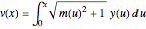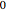用表示从到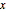的势能部分.

In[5]:=

varsv = Array[v, nh + 1, {0, nh}];

用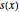表示链条在位置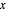的长度，并为之设置变量.

In[6]:=

varss = Array[s, nh + 1, {0, nh}];

将所有变量结合在一起.

In[7]:=

vars = Join[varsm, varsy, varsv, varss];

我们的目的是将势能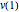最小化.

In[8]:=

objfn = v[nh];

下面是由几何形状决定的边界值约束.

In[9]:=

bndcons = {y[0] == a, y[nh] == b, v[0] == 0, s[0] == 0, s[nh] == L};

将常微分方程 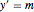, , 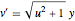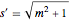离散化.

In[10]:=

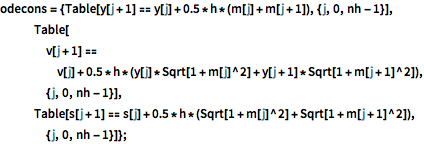
odecons = {Table[
    y[j + 1] == y[j] + 0.5*h*(m[j] + m[j + 1]), {j, 0, nh - 1}],
   Table[v[j + 1] == 
     v[j] + 0.5*
       h*(y[j]*Sqrt[1 + m[j]^2] + y[j + 1]*Sqrt[1 + m[j + 1]^2]), {j, 
     0, nh - 1}], 
   Table[s[j + 1] == 
     s[j] + 0.5*h*(Sqrt[1 + m[j]^2] + Sqrt[1 + m[j + 1]^2]), {j, 0, 
     nh - 1}]};

选取变量的初始点.

In[11]:=

tmin = If[b > a, 0.25 , 0.75]; init = 
 Join[Table[4*Abs[b - a]*((k/nh) - tmin), {k, 0, nh}],
  Table[4*Abs[b - a]*(k/nh)*(0.5*(k/nh) - tmin) + a, {k, 0, nh}],
  Table[(4*Abs[b - a]*(k/nh)*(0.5*(k/nh) - tmin) + a)*4*
    Abs[b - a]*((k/nh) - tmin), {k, 0, nh}], 
  Table[4*Abs[b - a]*((k/nh) - tmin), {k, 0, nh}]];

在满足约束的条件下将势能最小化.

In[12]:=

sol = FindMinimum[{objfn, Join[bndcons, odecons]}, 
   Thread[{vars, init}]];

提取解.

In[13]:=

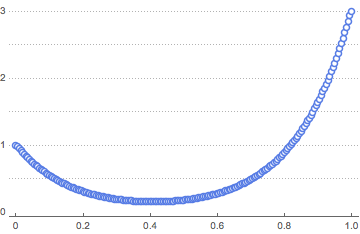
solpts = Table[{i h, y[i] /. sol[[2]]}, {i, 0, nh}];

绘制势能最小时链条位置的图形.

In[14]:=

ListPlot[solpts, ImageSize -> Medium, PlotTheme -> "Marketing"]

Out[14]=

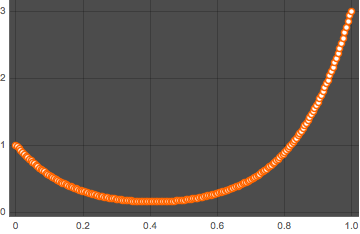
用 FindFit 将结果与悬链曲线拟合.

In[15]:=

catenary[t_] = c1 + (1/c2) Cosh[c2 (t - c3)];

In[16]:=

fitsol = FindFit[solpts, catenary[t], {c1, c2, c3}, {t}]

Out[16]=

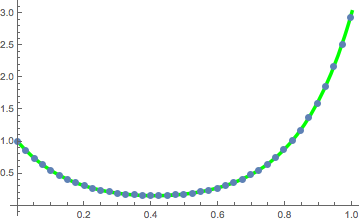
同时绘制解及悬链曲线.

In[17]:=

Show[Plot[catenary[t] /. fitsol, {t, 0, 1}, 
  PlotStyle -> Directive[Green, Thickness[0.01]], 
  ImageSize -> Medium], 
 ListPlot[Take[solpts, 1 ;; nh ;; 5], PlotStyle -> PointSize[.02]]]

Out[17]=

Wolfram 语言™

建立一个吊链模型

相关范例