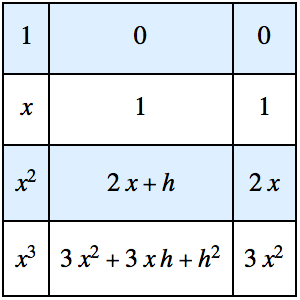
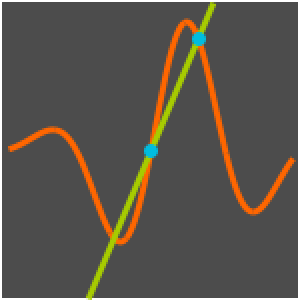
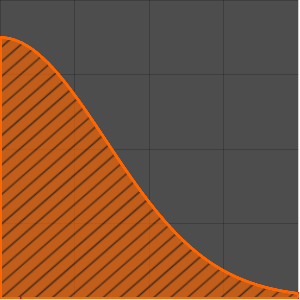
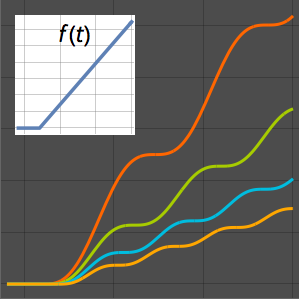
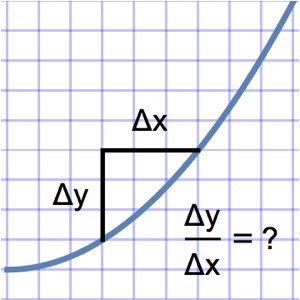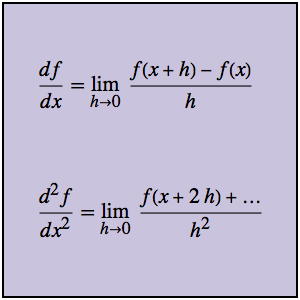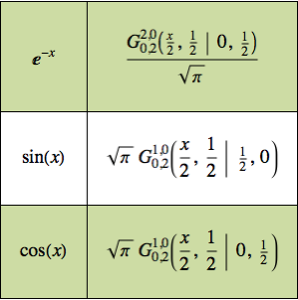Modélisez une chaîne pendante
Trouvez la position avec l'énergie potentielle minimale d'une chaîne ou d'un fil de longueur 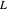 suspendue entre deux points.
suspendue entre deux points.
Configurez les valeurs de paramètre de la longueur de la chaîne 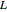 , la hauteur de l'extrémité gauche
, la hauteur de l'extrémité gauche 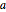 et la hauteur de l'extrémité droite
et la hauteur de l'extrémité droite 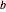 .
.
L = 4; a = 1; b = 3; Soit 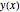 , la hauteur de la chaîne comme fonction de position horizontale, avec
, la hauteur de la chaîne comme fonction de position horizontale, avec 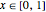 .
.
xf = 1; nh = 201; h := xf/nh;Configurez les variables pour la hauteur de la chaîne 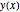 .
.
varsy = Array[y, nh + 1, {0, nh}];Désignez la pente à la position 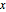 par
par 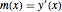 et configurez-lui des variables.
et configurez-lui des variables.
varsm = Array[m, nh + 1, {0, nh}];Désignez l'énergie potentielle partielle de 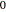 à
à 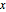 par
par 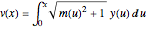 .
.
varsv = Array[v, nh + 1, {0, nh}];Désignez la longueur de la chaîne à la position 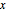 par
par 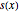 et configurez-lui des variables.
et configurez-lui des variables.
varss = Array[s, nh + 1, {0, nh}];Joignez toutes les variables.
vars = Join[varsm, varsy, varsv, varss];L'objectif est de minimiser l'énergie potentielle totale 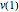 .
.
objfn = v[nh];Voici la valeur limite des contraintes géométriques.
bndcons = {y[0] == a, y[nh] == b, v[0] == 0, s[0] == 0, s[nh] == L}; Discrétisez les EDO : 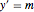 ,
, 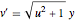 ,
, 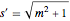 .
.
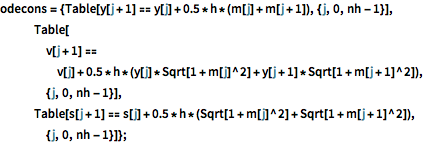
odecons = {Table[
y[j + 1] == y[j] + 0.5*h*(m[j] + m[j + 1]), {j, 0, nh - 1}],
Table[v[j + 1] ==
v[j] + 0.5*
h*(y[j]*Sqrt[1 + m[j]^2] + y[j + 1]*Sqrt[1 + m[j + 1]^2]), {j,
0, nh - 1}],
Table[s[j + 1] ==
s[j] + 0.5*h*(Sqrt[1 + m[j]^2] + Sqrt[1 + m[j + 1]^2]), {j, 0,
nh - 1}]};Choisissez des points initiaux pour les variables.

tmin = If[b > a, 0.25 , 0.75]; init =
Join[Table[4*Abs[b - a]*((k/nh) - tmin), {k, 0, nh}],
Table[4*Abs[b - a]*(k/nh)*(0.5*(k/nh) - tmin) + a, {k, 0, nh}],
Table[(4*Abs[b - a]*(k/nh)*(0.5*(k/nh) - tmin) + a)*4*
Abs[b - a]*((k/nh) - tmin), {k, 0, nh}],
Table[4*Abs[b - a]*((k/nh) - tmin), {k, 0, nh}]];Minimisez l'énergie potentielle totale, sous réserve des contraintes.
sol = FindMinimum[{objfn, Join[bndcons, odecons]},
Thread[{vars, init}]];Extrayez les points de solution.
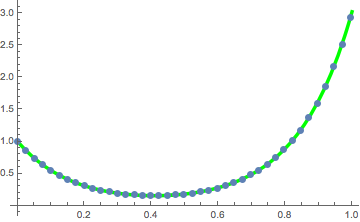
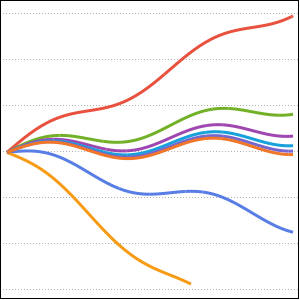
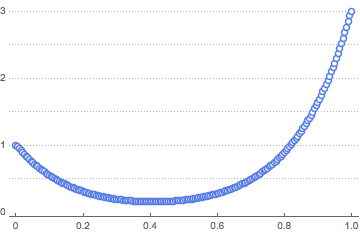
solpts = Table[{i h, y[i] /. sol[[2]]}, {i, 0, nh}];Tracez la position de la chaîne avec un minimum d'énergie potentielle.
ListPlot[solpts, ImageSize -> Medium, PlotTheme -> "Marketing"]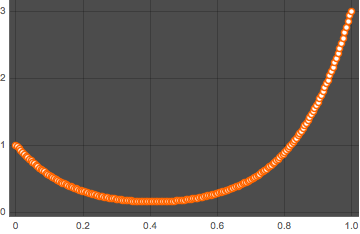
Utilisez FindFit pour adapter le résultat à la courbe caténaire.
catenary[t_] = c1 + (1/c2) Cosh[c2 (t - c3)];fitsol = FindFit[solpts, catenary[t], {c1, c2, c3}, {t}]Tracez les points de solution avec la courbe caténaire.

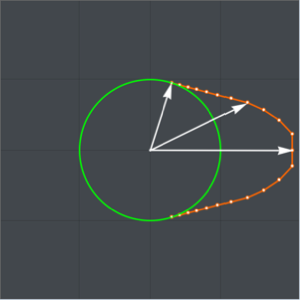
Show[Plot[catenary[t] /. fitsol, {t, 0, 1},
PlotStyle -> Directive[Green, Thickness[0.01]],
ImageSize -> Medium],
ListPlot[Take[solpts, 1 ;; nh ;; 5], PlotStyle -> PointSize[.02]]]