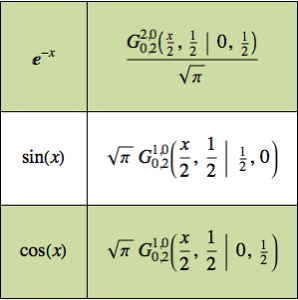垂れ下がった鎖をモデル化する
2点の間に垂れ下がった長さ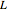 
の鎖あるいは紐が最小ポテンシャルエネルギーを持つ位置を求める．
鎖の長さ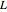 
，左端の高さ 
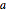，右端の高さ 
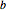に対するパラメータ値を設定する．
In[1]:=
L = 4; a = 1; b = 3;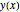 
を 
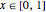である水平位置の関数としての鎖の長さとする．
In[2]:=
xf = 1; nh = 201; h := xf/nh;鎖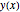 
の高さに対する変数を設定する．
In[3]:=
varsy = Array[y, nh + 1, {0, nh}];位置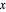 
での勾配を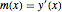 
で表し，それに対する変数を設定する．
In[4]:=
varsm = Array[m, nh + 1, {0, nh}];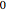
から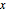 
までの部分的なポテンシャルエネルギーを 
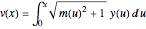で表す．
In[5]:=
varsv = Array[v, nh + 1, {0, nh}];位置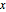 
での鎖の長さを 
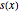で表し，それに対する変数を設定する．
In[6]:=
varss = Array[s, nh + 1, {0, nh}];すべての変数を繋ぐ．
In[7]:=
vars = Join[varsm, varsy, varsv, varss];この目的は，全ポテンシャルエネルギー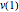 
を最小化することである．
In[8]:=
objfn = v[nh];次は幾何学からの境界値制約条件である．
In[9]:=
bndcons = {y[0] == a, y[nh] == b, v[0] == 0, s[0] == 0, s[nh] == L};常微分方程式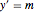 
, 
, 
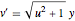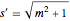を離散化する．
In[10]:=
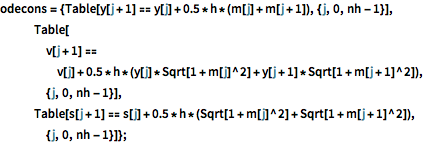
odecons = {Table[
y[j + 1] == y[j] + 0.5*h*(m[j] + m[j + 1]), {j, 0, nh - 1}],
Table[v[j + 1] ==
v[j] + 0.5*
h*(y[j]*Sqrt[1 + m[j]^2] + y[j + 1]*Sqrt[1 + m[j + 1]^2]), {j,
0, nh - 1}],
Table[s[j + 1] ==
s[j] + 0.5*h*(Sqrt[1 + m[j]^2] + Sqrt[1 + m[j + 1]^2]), {j, 0,
nh - 1}]};変数に対する初期点を選ぶ．
In[11]:=
tmin = If[b > a, 0.25 , 0.75]; init =
Join[Table[4*Abs[b - a]*((k/nh) - tmin), {k, 0, nh}],
Table[4*Abs[b - a]*(k/nh)*(0.5*(k/nh) - tmin) + a, {k, 0, nh}],
Table[(4*Abs[b - a]*(k/nh)*(0.5*(k/nh) - tmin) + a)*4*
Abs[b - a]*((k/nh) - tmin), {k, 0, nh}],
Table[4*Abs[b - a]*((k/nh) - tmin), {k, 0, nh}]];制約条件の対象となる全ポテンシャルエネルギーを最小化する．
In[12]:=
sol = FindMinimum[{objfn, Join[bndcons, odecons]},
Thread[{vars, init}]];解の点を抽出する．
In[13]:=
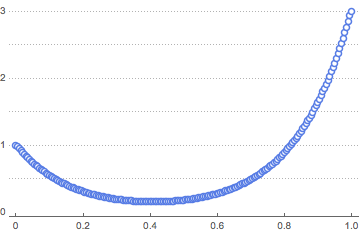
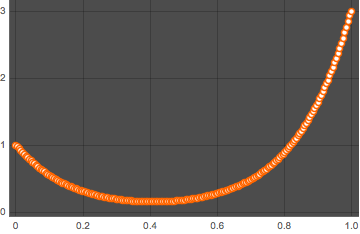
solpts = Table[{i h, y[i] /. sol[[2]]}, {i, 0, nh}];最小ポテンシャルエネルギーを持つ鎖の位置をプロットする．
In[14]:=
ListPlot[solpts, ImageSize -> Medium, PlotTheme -> "Marketing"]Out[14]=
FindFitを使って，懸垂曲線に結果をフィットする．
In[15]:=
catenary[t_] = c1 + (1/c2) Cosh[c2 (t - c3)];In[16]:=
fitsol = FindFit[solpts, catenary[t], {c1, c2, c3}, {t}]Out[16]=
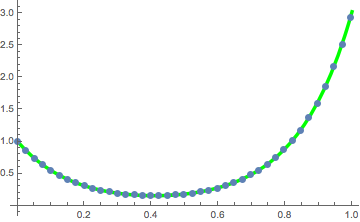
解の点と懸垂曲線を一緒にプロットする．
In[17]:=
Show[Plot[catenary[t] /. fitsol, {t, 0, 1},
PlotStyle -> Directive[Green, Thickness[0.01]],
ImageSize -> Medium],
ListPlot[Take[solpts, 1 ;; nh ;; 5], PlotStyle -> PointSize[.02]]]
Out[17]=
