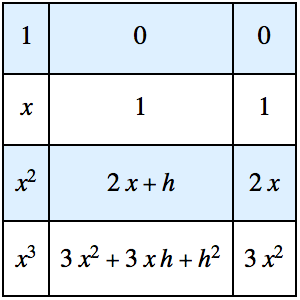
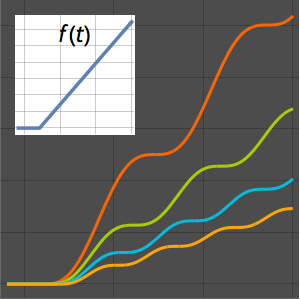
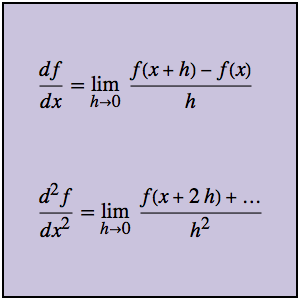用格林函数解初始值问题

用 GreenFunction 求解非齐次微分方程的初始值问题.

首先计算格林函数.

In[1]:=

gf[s_, t_] = GreenFunction[{-u''[t] + u'[t] - 37/4 u[t], u[0] == 0, u'[0] == 0}, u[t], {t, 0, \[Infinity]}, s]

Out[1]=

定义力函数.

In[2]:=

f[t_] := Cos[a t]

格林函数与力函数的卷积给出方程的解.

In[3]:=

sol = Integrate[gf[s, t] f[s], {s, 0, \[Infinity]}, Assumptions -> t > 0]

Out[3]=

与 DSolveValue 给出的结果比较.

In[4]:=

DSolveValue[{-u''[t] + u'[t] - 37/4 u[t] == f[t], u[0] == 0, u'[0] == 0}, u[t], t] // FullSimplify

Out[4]=

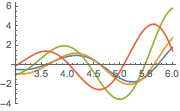
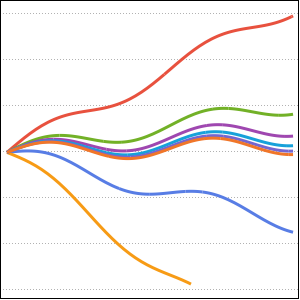
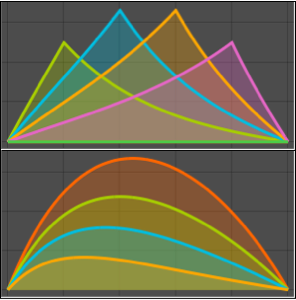
绘制参数 a 取不同的值时解的图形.

In[5]:=

Plot[Table[sol, {a, 1, 4, 0.8}] // Evaluate, {t, 3, 6}]

Out[5]=