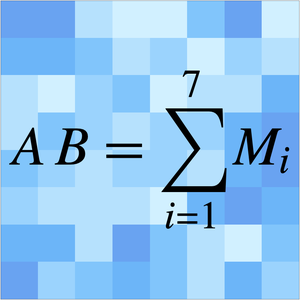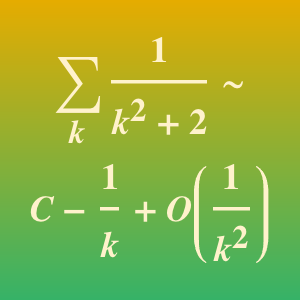Déterminez la complexité d'un calcul
Quand on parle du temps d'exécution d'un algorithme, il est conventionnel de donner la fonction la plus simple AsymptoticEqual (grand 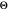 ) de la fonction d'exécution exacte. Une autre façon d'affirmer cette égalité est de dire que chaque fonction est à la fois AsymptoticLessEqual (grand
) de la fonction d'exécution exacte. Une autre façon d'affirmer cette égalité est de dire que chaque fonction est à la fois AsymptoticLessEqual (grand 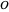 ) et AsymptoticGreaterEqual (grand
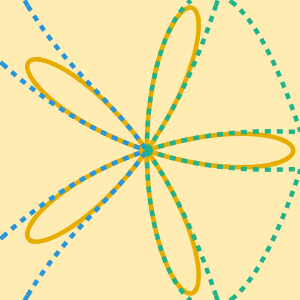
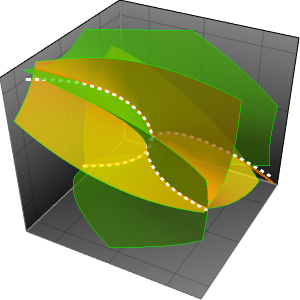
) et AsymptoticGreaterEqual (grand 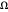 ) par rapport à l'autre. Ces concepts sont illustrés dans le contexte de l'algorithme de Strassen, le premier algorithme de multiplication de matrice sous-cubique.
) par rapport à l'autre. Ces concepts sont illustrés dans le contexte de l'algorithme de Strassen, le premier algorithme de multiplication de matrice sous-cubique.
L'algorithme comprend quatre étapes : diviser chacune des matrices 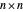 en 4 sous-matrices, former 14 combinaisons linéaires à partir des 8 sous-matrices, multiplier 7 paires de celles-ci et additionner les 7 résultats. Le temps
en 4 sous-matrices, former 14 combinaisons linéaires à partir des 8 sous-matrices, multiplier 7 paires de celles-ci et additionner les 7 résultats. Le temps 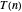 utilisé pour faire la multiplication sera donc un temps constant
utilisé pour faire la multiplication sera donc un temps constant 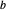 pour diviser la matrice,
pour diviser la matrice, 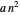 pour former des combinaisons linéaires dans les deuxième et quatrième étapes et
pour former des combinaisons linéaires dans les deuxième et quatrième étapes et 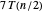 pour la troisième étape.
pour la troisième étape.
Résolvez la relation de récurrence.
Bien que le résultat soit compliqué, 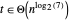 .
.
En conséquence, 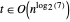 et
et 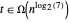 .
.
Remarquez que 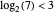 , l'algorithme est alors sous-cubique.
, l'algorithme est alors sous-cubique.
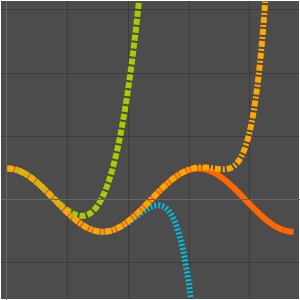
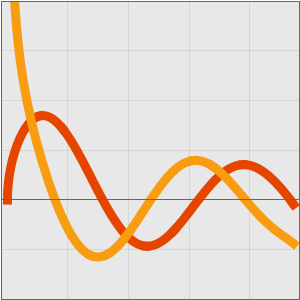
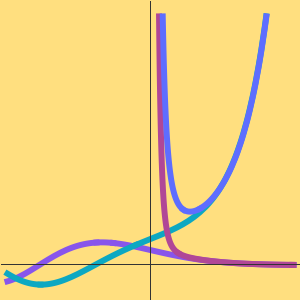
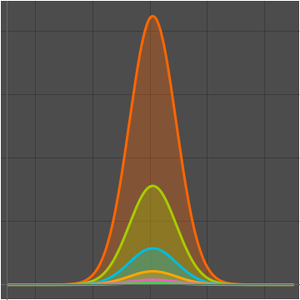
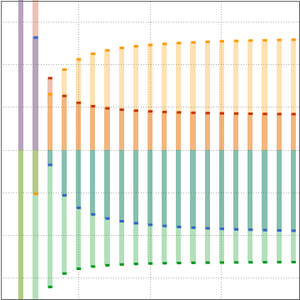
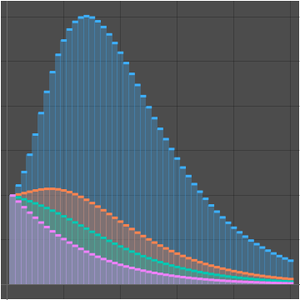
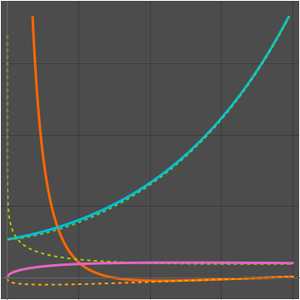
Comparez le taux de croissance de l'algorithme cubique naïf et celui de l'algorithme de Strassen.